chalte chalte find the area

good lord[7][7]........i never hoped a mind built question would have such ingenous solution

Though i'm not getting a very nice integral, kaymant sir may turn out to be helpful hereWell I wanted to do by another way other than polar co-ordinates, so I rotated the axes!

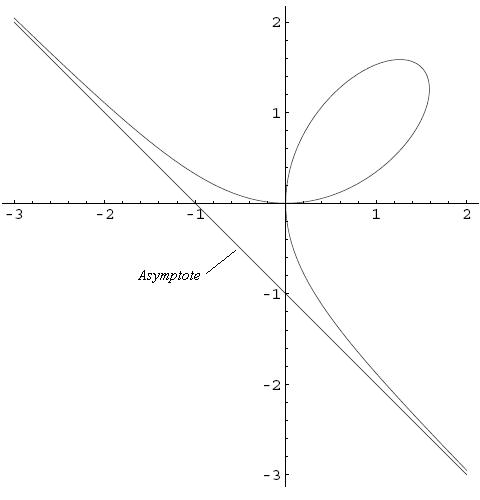
since the graph passes through the origin, and yet we have it symmetric about the line y=x, we rotate the axes in an anticlockwise manner by \frac{\pi}{4}

So x=\frac{X}{\sqrt{2}}+\frac{Y}{\sqrt{2}}\\ \ y=\frac{X}{\sqrt{2}}-\frac{Y}{\sqrt{2}}
New eqn thus becomes
3Y^2(\sqrt{2}X+1)=3X^2-\sqrt{2}X^3\\ \ Y=\pm \sqrt{\frac{3X^2-\sqrt{2}X^3}{3(\sqrt{2}X+1)}
That further gives that graph is symmetric abt the X-axis in our new co-ordinate system,
AS D→0, Y→∞, so X=\frac{-1}{\sqrt{2}}
forms the asymptote.

Ultimately this is the integral that i get - and the one i need help in evaluating....

\int_{0}^{\frac{3}{\sqrt{2}}}\sqrt{\frac{3X^2-\sqrt{2}X^3}{\sqrt{2}X+1}}dx
someone pls evaluate this!