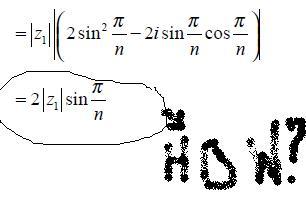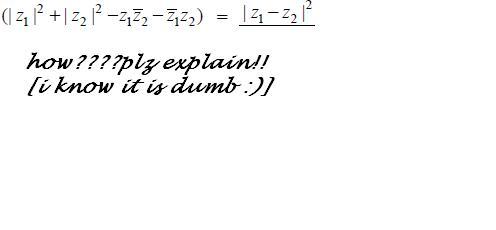HEY PLZ REPLY!!!!
10 Answers
|z1|*|2|*|sin(pi/n)|*|sin(pi/n) - icos(pi/n)|
= 2|z1|*|sin(pi/n)|*1
I KNOW I M BEING DUMB.......BUT THT ONLY M NOT GETTING HOW
IS IT 1.......OK OK...................GOT IT SIN2+COS2=1......[1]...SORRY
YAAR DIMAAG MEIN JUNG LAG GAYA HAI[2]
|z1|2+|z2|2 - z1 z2 - z1 z2
=z1 z1+z2 z2 - z1 z2 - z1 z2
=z1 (z1 - z2) - z2 (z1 - z2)
=(z1 - z2) (z1 - z2)
=(z1 - z2)(z1 - z2)
=|z1 - z2|2
z1= x+iy
z2=a+ib
z1=x-iy
z2=a-ib
z1+z2=(a+x)+i(b+y)
z1+z2=(a+x)+i(-b-y)=(a+x)-i(b+y)=z1+z2
yaar lagta hai tough problems solve karte karte i m forgetting basics[2][2]
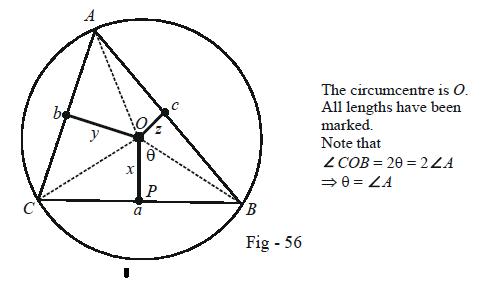
for O to be the circumcentre, it must be equidistant from A, B and C...thus,
umm......it must lie on the perpendicular bisectors of AB, BC and CA....
OP is perpendicular on BC(figure suggests!![3][3]) thus OP must be BC's perp bisector!!
now in ΔOPC and ΔOPB,
OP =OP (common)
CP =BP (OP is perp bisector of BC)
OC =OB (radius of same circle)
thus ΔOPC ≡ ΔOPB
thus <COP = <BOP=θ
thus <COB=<COP + <BOP = 2θ