341pls check the denominator of the arg expression
let Zr,r=1,2,3.....n are n distinct roots of eq ^{n}C_{1}x+^{n}C_{2}x^{2}+^{n}C_{3}x^{3}+.......^{n}C_{n}x^{n}=0 in argand plane.If der exist exactly one Zr, rε{1,2....n} such that arg\left(\frac{Z_{r}-(-1+\sqrt{2}i}{(-1)-(-1+\sqrt{2}i)} \right)=\frac{\pi }{4} then n can be ??
-
UP 0 DOWN 0 0 4
4 Answers
1
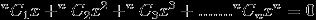is the same as (x+1)n=1
The solution to this lies on the red circle in the fig.
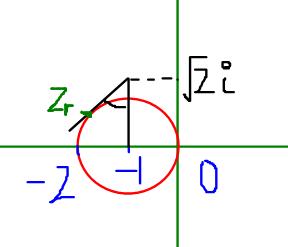
zr is a point such that, arg(-1+√2i - zr)=∩/4
This when solved, along with the eqn of circle, |z+1|=1 or by using simple geometry gives zr= ei3∩/4-1
This when substituted in the eqn gives, (ei3∩/4)n/r=1
=> 3∩n/4 = 2∩ , or n/r=8/3,
This gives n=8 and ei3∩/4-1 is the third root anti-clockwise...........
[339]