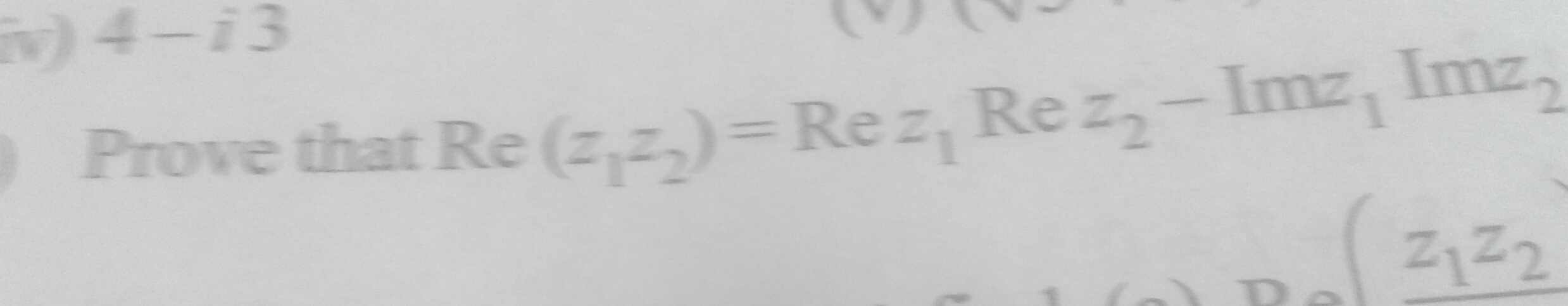complex no.

\mathbf{z_{1}=r_{1}e^{i\theta_{1}},}\mathbf{z_{2}=r_{2}e^{i\theta_{2}}}

Use,
e^iθ=cosθ+isinθ

And find z₁z₂.You'll find that:

\mathbf{Re(z_{1}z_{2})=r_{1}r_{2}(cos(\theta_{1})cos(\theta_{2})-sin(\theta_{1})sin(\theta_{2}))}

=\mathbf{r_{1}cos(\theta_{1})r_{2}cos(\theta_{2})-r_{1}sin(\theta_{1})r_{2}sin(\theta_{2})}

\mathbf{Re(z_{1})Re(z_{2})-Im(z_{1})Im(z_{2})}