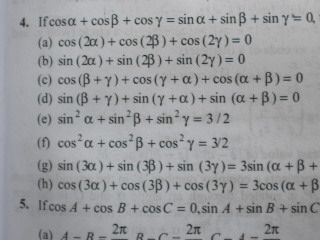Complex no.

2 Answers

535

Aditya Agarwal ·2014-02-06 13:47:04

let Z=e^{i(Î±+Î²+Î³)}=0
therefore, cosÎ±+cosÎ²+cosÎ³=0 & sinÎ±+sinÎ²+sinÎ³=0

Z²=0(Z=0)
therefore, e^{2i(Î±+Î²+Î³)}=0
or e^{i(2Î±+2Î²+2Î³)}=0
therefore, cos2Î±+cos2Î²+cos2Î³=0 & sin2Î±+sin2Î²+sin2Î³=0

Since,e^{i(2Î±+2Î²+2Î³)}=0
therefore, e^{i{(Î±+Î²)+(b+Î³)+(Î³+Î±)}}=0
So. cos(Î±+Î²)+cos(b+Î³)+cos(b+Î³)=0 & sin(Î±+Î²)+sin(b+Î³)+sin(Î³+Î±)=0

UP 2 DOWN 2
Himanshu Giria thanx ... quite a small method .....
Upvote·0· Reply ·2014-02-06 17:47:53
Aditya Agarwal i dont think this is correct. e^[i(2Î±+2Î²+2Î³)] should be equal to cos(2Î±+2Î²+2Î³) and so on and so forth...
Upvote·0· Reply ·2014-02-06 19:45:51
Post on FacebookPost anonymously?

591

Akshay Ginodia ·2014-02-05 04:44:55

Take z₁=cosÎ±+isinÎ±
z₂=cosÎ²+isinÎ²
z₃=cosÎ³+isinÎ³

so, z1+z2+z3 = cosÎ±+cosÎ²+cosÎ³ + i(sinÎ±+sinÎ²+sinÎ³)=0
and 1z1= CosÎ± - isinÎ± (from demoivre's theorem)
similarly for others..
so , 1z1+1z2+1z3=0

now z₁² + z₂² + z₃² = (z1+z2+z3)² - 2(z1z2 + z2z3 + z3z1)
=0 + 2z1z2z3(1z1+1z2+1z3) = 0
now z₁² + z₂² + z₃² = e^i2Î± + e^i2Î² + e^i2Î³ = 0

Equate the real and complex part to zero for 1st two..when u get cos2Î±+cos2Î²+cos2Î³= 0 use the formula for cos2x to get (e) and (f) part..

Then take (z1+z2+z3)² = 0 and equate the complex and real parts to zero for (c) and (d)

For (g) and (h) u will have to find z1³+ z2³+z3³ ...:)

If u find a shorter method please tell me too..

√ √ || {} [] () → ~ ^ x x x → → ln log lg lim lim cos sin tan cot arcsin arccos arctan

∫ ∫ ∫ ∫ ∫ ∬ ∬ ∬ ∬ ∬ ∭ ∭ ∭ ∭ ∭ ⨌ ⨌ ⨌ ⨌ ⨌

∑ ∑ ∑ ∑ ∑ ∮ ∮ ∮ ∮ ∮ ∏ ∏ ∏ ∏ ∏ ∐ ∐ ∐ ∐ ∐

+ - × ÷ ± ∓ = ∪ ∩ ≠ ∼ ≈ ∅ ∀ ∃ ∈ ∋ ∝ ≤ ≥ ≃ ≅ ≡ < > ≪ ≫ ⊂ ∉ ⊃ ⊆ ⊇ ⇒ ⇐ ⇔ ⇒ ⇐ ⇔ ⇑ ⇓ ⇕ → ← ↔ → ← ↔ ↑ ↓ ↕ ↖ ↗ ↘ ↙ ↪ ↩ ⇀ ↼ ⇁ ↽

° ∂ ∞ α β γ δ θ λ μ ν ξ π ρ σ φ ω ε ƒ κ τ υ Γ Δ Λ Σ Π Ω