Complex Number

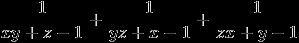
HINT:

The expr. can be written as ....

zxyz + z² - z + xxyz + x² - x + yxyz + y² - y

That can be further written as ....

z4 + z² - z + x4 + x² - x + y4 + y² - y

Now .... try to solve ....

x,y,z are the roots of a polynomial, f(t) = t^3-\left(\sum x\right) t^2 + \left(\sum xy\right) t-xyz
We are already given\sum x = 2; xyz=4. And from the second relation

\sum xy = \frac{(\sum x)^2 - \sum x^2}{2} = \frac{1}{2}

So the polynomial is t^3-2t^2+\frac{t}{2}-4 \equiv (t-x)(t-y)(t-z)
Now, \sum \frac{1}{xy+z-1} = \sum \frac{1}{xy +1 -x-y} = \sum \frac{1}{(1-x)(1-y)} = \frac{f'(1)}{f(1)}

f(1) = -\frac{9}{2};f'(1) = -\frac{1}{2}

Hence the given expression equals \frac{1}{9}