dudericky...did u realize....why i posted just "this case"....because in this case "angle bisectors as they often tend to be one and the same ".........but in this case they are not same....[1]
12 Answers
I ' ll give a " one - size - fits - all " solution which ' ll take care of " the case " mentioned above .
See , whenever you have to prove that equality of angles in pairs of straight lines , you must look at the corresponding angle bisectors as they often tend to be one and the same . Here also , the angle bisector of the first pair of lines : -
L1' ≡ x 2 - y 2a - b = x yh
Similarly , angle bisector of the second pair of lines : -
L2' ≡ x 2 - y 2( a + λ ) - ( b + λ ) = x 2 - y 2a - b = x yh
Since , L1' ≡ L2' ;
Hence , the angle contained in between one line of the first pair and one line of the second pair is the same as that contained in between the other line of the first pair and the other line of the second pair .
waise i solved by same method u told....but it is only valid for remaining two cases as u would have realized by now...this third possiility still prevails which is not resolved by this approach!
@ricky
have a hitch tht u are right
but i did not get wat u said in above post no. 5 can u plz elaborate more...n explain why this case does not exist
thanks
The equation of the angle bisectors -
h ( x 2 - y 2 ) + x y ( b - a ) = 0
The equation of the second pair of lines -
a x 2 + 2 h x y + b y 2 + λ ( x 2 + y 2 ) = 0
For these two to be equivalent , compare the co - efficients : -
a + λ = h .............. ( 1 )
b + λ = - h .................. ( 2 )
And , b - a = 2 h ................ ( 3 )
Subtracting ( 1 ) from ( 2 ) ,
b - a = - 2h ................... ( 4 )
( 3 ) and ( 4 ) are consistent only if ,
b = a
But that cannot happen since then , " h = 0 " , which again , is impossible .
Hence , the situation described as above is impossible .
@kunl , in " this case " , the second pair of lines are the angle bisectors of the first pair of lines and vice - versa
but in this figure i can't see how second pair is bisector of angles of first pair?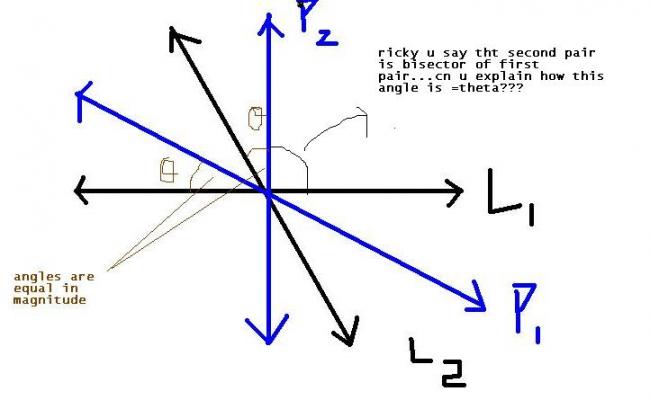
Let the point of intersection of 3 lines be ( c , d ) .
Then , a c 2 + 2 h c d + b d 2 = 0
And , a c 2 + 2 h c d + b d 2 + λ ( a 2 + b 2 ) = 0
Subtracting these two equations ,
λ ( a 2 + b 2 ) = 0
So , λ = 0
But that cannot happen .
Hence , the diagram you drew is not possible .
but the equation are second degree homogeneouys as well so they do intersect at origin...so now only possibility tht prevails is this
1.IF AT ALL QUESTION IS TO BE RIGHT it is a "DEGENERATE:" case...i.e. two pairs are identical[3][3]
2.Else Question itself is wrong!!!!!!
well the quesn , especially the diagram , looks strange to me!!
i too feel it isnt possible............:P
but its just a feeling only!!
:P
ricky i m gonna kill u....why did u delete tht image which u posted?...it would have clarified matter to others too :P[3][3]
