71let the infinite term be y.then
log7log7y
taking log on an indefinite i.e.,∞ no. gives infinite no. so,
log7log7y = y
1nihal what are the given options????
just solve ur self ...the equation is :
y = log7log7(Z)
z = \sqrt{z+7}
z^{2} = z + 7
z^{2}-z-7=0
z = \frac{1 +- \sqrt{1^{2} -(4*7*1)}}{2}
z = \frac{1 +-\sqrt{29}}{2}
z = 1 - √292 is discarded as it is less than 1
so z = 1 + √292
1acc to pritishmast ans should be -0.265 but it is not in the options means that method is wrong as cal. are correct.....
qwerty can u or anyone solve this and give me the answer with ofcourse correct method........
23wat i mean is , u cant apply analogy anywhere randomly, i hope u get wat i m trying to say
btw if u assumed something , then check whether the ans is within your assumption. i.e , u assumed y to be infintely large, but it actually came out to be 1-3log2 , so the final ans is contradictory to the assumption , so the assumption shud be wrng
231-3log2 is not ∞
and 2 + (1-3log2 ) ≠1-3log2
u applied a concept , do u kno the basics of dat concept ?
1i have used here the concept we apply in infinite serirs of resistors or capacitors...u remember.....
taking logarithm on an indefinite number will also be indefinite like 2+∞=∞ and much more....
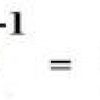1@ Nihal
Let z = \sqrt{7+\sqrt{7+\sqrt{7+......infinity}}}
Now cover the first square root to get
\sqrt{7+\sqrt{7+......infinity}} which is also equal to z
(i.e.) \sqrt{7+\sqrt{7+......infinity}} = z
Therefore z =\sqrt{7+z}
Square both sides 2 get a quadratic in z
23@ nihal , why do u think that y is an infinite number ?
and also , if u assumed it to be an infinite number , did it turn out to be infinite ?
u said log7log7y= y
is ur answer y = 1-3log2 satisfying it ?
@ pritishmast i think wat u have done is correct if calc are correct
1if acc. to u log7log7y=y is not possible then how can be - z=√z+7 possible in ur solution???
1ans will be -0.265 only unless i haven''t made any calculation mistakes
@vivek
harry is correct
the complex looking number \sqrt{7+\sqrt{7+\sqrt{7+.........infinity}}} is not undefined or infinity .....it has a definite value.....calculating the value of this number
is just a simple 10th class problem.... only extra logarithm concept has been added
1according to given solution ans will be same for every question like that
i.e. log7log7y=y
for any value of y which is an ∞ series
Ex.
y=">
1how can you take log7log7√7+√7+√7....∞ =y
and also √7+√7+√7....∞ =y
1solution....
let the infinite term be y.then
log7log7y
taking log on an indefinite i.e.,∞ no. gives infinite no. so,
log7log7y = y
differentiating both sides w.r.t. y gives
1log7y X log7e X 1y X log7e=1
log7logy X logelog7 X 1y X logelog7=1
1logy.log7.y=1
y.logy=1log7
again differentiating w.r.t. y
1 + logy =0
logy=-1
y=110
y=.1
or y=1-3log2
that is the answer.....
1oh so it is like this:
\sqrt{7+\sqrt{7+\sqrt{7+\sqrt{7+\sqrt{7}}}}..............infinity }
let y=log7log7(z)
where z = \sqrt{7+\sqrt{7+\sqrt{7+\sqrt{7+\sqrt{7}}}}..............infinity }
or z = \sqrt{7+z}
solving this we get z= 1±√292
z=1-√292 neglected because
log7(1-√292 )=undefined as 1-√292 < 0
so z= 1+√292
so required value of y = log7log7(1+√292)
y = -0.265
1hey, (7+......∞)≠(7+8+9+....∞)
dots signify that the series continues....
7+....∞={7+[7+(7+....∞)1/2]1/2}1/2
now solve it..........
1is that 7+.....∞ =7 + 8 + 9 + 10........+ ∞ ???
donno why im getting answer ∞
