1) Solution of inequality 2|x+1| > x+4 contains which interval?
2) If R is a relation from a finite set A having m elements to a finite set B having n elements, then find the number of relations from A to B.(with proof)
Function ka Concept pura nehi samjha i think. i can just put value of x in any function but cant do sums lyk
!) A cylinder is inscribed in a sphere of radius R while the volume V of the cylinder is written as V=f(x), where x is the height of cylinder. The function V/x represents what ?
st.line or a circle or increasing functn or decreasing?
492)
relation means a set of all possible (a,b) where aεA and bεB
a can be chosen in m ways.
b can be chosen in n ways for each a...
thus total of mn ordered pairs are possible..[1]
Now when we are building a function we can either take in one of the ordered pair or reject it to get lost! [3]
So each ordered pair can be treated in 2 ways...
thus net number of possible collection=2mn
but this includes when none is selected...i.e. a null set and it has to be ignored as it is not a relation..
thus total number of relations=2mn-1
30Whenever you see a modulus function, check where it becomes zero and solve separately where the term inside the mod is negative and when it is positive.
1) When x<1
-2x - 2 > x + 4
=> 3x < - 6
=> x < -2
When x≥1
2x + 2 > x + 4
x > 2
Hence required interval (-∞,-2) U (2,∞) . [1]
493)
for this sum i ll upload the figure of one section of the entire setup .. this section contains the axis of the cylinder in consideration! [1]
the section:
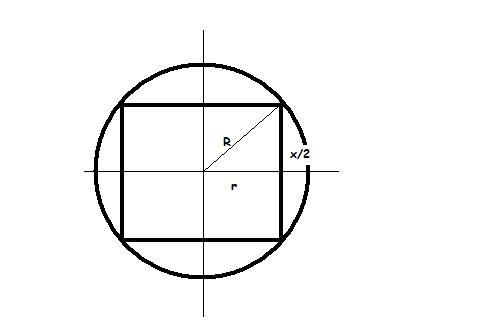
R=radius of the sphere
r=radius of cylinder
x=height of cylinder
from the right angled triangle,
r^2+\left(\frac{x}{2} \right)^2=R^2\\ or,\;r^2=\frac{4R^2-x^2}{4}
We know,
V(x)= \pi r^2x = \pi\left(\frac{4R^2-x^2}{4} \right)x\\ or,\;\frac{V(x)}{x} = \frac{\pi}{4}\left(4R^2-x^2 \right)
Now u decide from the options! [1]
7Let S={1,2,3,4}. What is the total number of unordered pair of disjoint subsets of S?
491) an unordered pair or pair set is a set of the form {a, b}, i.e. a set having two elements a and b with no particular relation between them. In contrast, an ordered pair (a, b) has a as its first element and b as its second element.
2) disjoint means the intersection of that 2 set is a null set!
3) null set is sub set of every set! [1]
49So these unordered pairs have 2 elements each of which is another set..
let the element sets be A and B
{n(A),n(B)} can be {0,1}, {0,2}, {0,3}, {1,1}, {1,2}
and none else (why?)
{n(A),n(B)} = {0,1} can be of 3 ways..
{n(A),n(B)} = {0,2) can be of 3 ways..
{n(A),n(B)} = {0,3} can be of 1 way..
{n(A),n(B)} = {1,1} can be of 3 ways..
{n(A),n(B)} = {1,2} can be of 3 ways..
thus net 13 ways..
Did I miss something out???
49sorry i took S={1,2,3}
anyway the essence of the solution remains the very same! [1]
So, the post thrives..
try solving out the original sum urself! [1]
211)
the meaning of modulus implies we need either 2x+2 ≥ x+ 4 or 2x+2≤-(x+2)