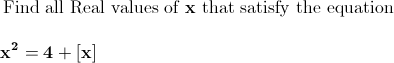Greatest integer function

\hspace{-16}$Given that $\bf{x^2=4+\left[x\right]}$\\\\\\ Now Using $\bf{x=\left[x\right]+\left\{x\right\}}$\\\\\\ So $\bf{x^2=4+x-\left\{x\right\}}$\\\\\\ So $\bf{\left\{x\right\}=-x^2+x+4}$\\\\\\ Using $\bf{0\leq \left\{x\right\}<1}$\\\\\\ So $\bf{0\leq -x^2+x+4 <1}$\\\\\\ So $\bf{x^2-x-4 \leq 0\;\; \cup \;\; x^2-x-3>0}$\\\\\\ So $\bf{\frac{1}{2}.\left(1-\sqrt{13}\right)\leq x \leq \frac{1}{2}.\left(1+\sqrt{13}\right)\;\; \cup\;\; \frac{1}{2}.\left(1-\sqrt{17}\right)< x<\frac{1}{2}.\left(1+\sqrt{17}\right)}$\\\\\\ So $\bf{\frac{1}{2}.\left(1-\sqrt{17}\right)\leq x < \frac{1}{2}.\left(1+\sqrt{13}\right)\;\; \cup \;\; \frac{1}{2}.\left(1+\sqrt{13}\right)< x \leq \frac{1}{2}.\left(1+\sqrt{17}\right)}$\\\\\\ So Integer values of $\bf{x}$ are i.e $\bf{[x]=-2\;\;,2}$\\\\\\ $\bf{\bullet}$ If $\bf{[x]=-2\Leftrightarrow -2 \leq x< -1}$.\\\\\\ Then $\bf{x^2=4-2=2\Leftrightarrow x = -\sqrt{2}}$\\\\\\

\hspace{-16}\bullet $ If $\bf{[x]= 2\Leftrightarrow 2 \leq x< 3}$.\\\\\\ Then $\bf{x^2=4+2=2\Leftrightarrow x = \sqrt{6}}$\\\\\\ So $\bf{x\in \left\{-\sqrt{2}\;\;,\sqrt{6}\right\}}$

I proceeded in this way.....
→x^2=4+x-{x}
→{x}=x-x^2+4

Now we know dat 0≤{x}<1
So...... 0≤x-x^2+4<1
After this,we get an eq. as x-x^2+4≥0 or,x(x-1)≥-4
And another eq. as x(x-1)<-3
Now i am getting confused.....I could have proceeded but i am getting dat ganda wala answer......However d answer is (-√2,√6)