this has already been done as QOD
On the request of grandmaster.....writing some inequalities here which are no way necessary for JEE but can just reduce ur work
The Cauchy-Schwarz Inequality
(x1² + x2² + x3²)(y1² + y2² + y3²) ≥ (x1y1 + x2y2 + x3y3)², for reals xi and yj
Proof:
Considering the quadratic in t,
(tx1 + y1)² + (tx2 + y2)² + (tx3 + y3)²
=> t²(x1²+x2²+x3²) + 2t(x1y1+x2y2+x3y3) + (y1²+y2²+y3²)
which is greater than zero
because it's a sum of squares, so only one root=> b² - 4ac = 0,
OR no real roots at all, => b² - 4ac < 0.
Discriminant=D=4(x1y1+x2y2+x3y3)² - 4(x1²+x2²+x3²)(y1²+y2²+y3²)
D must be less than or equal to zero
(x1² + x2² + x3²)(y1² + y2² + y3²) ≥ (x1y1 + x2y2 + x3y3)², for reals xi and yj
Hence proved
-
UP 0 DOWN 0 0 9

9 Answers
The Chebyshev Sum Inequality
If a1 ≥ a2 ≥ ... ≥ an and b1 ≥ b2 ≥ ... ≥ bn then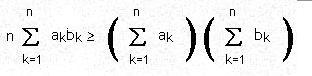
Proof
RHS :
Write it as a sum in this way
(a1b1 + a2b2 + ... + an-1bn-1 + anbn) +
(a1b2 + a2b3 + ... + an-1bn + anb1) +
...
(a1bn + a2b1 + ... + an-1bn-2 + anbn-1)
Using rearrangemnet inequality here we get the final result
Sorry mathie didnt know that.................[2][2]
grandmaster told me to write them and their proofs so i did the same
open that website, its only for inequalities, u will find many mind boggling inequalities there
for those who could not see the above one clearly, the website is http://jipam.vu.edu.au/
thanx for that link...........vaise there are lot of other links too.....[1]