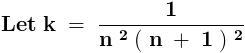
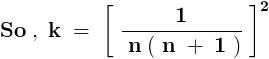

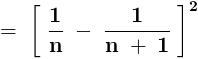
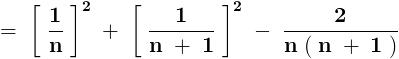
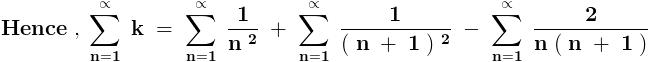
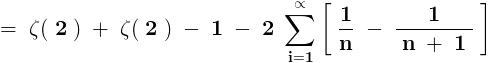
After telescoping ,
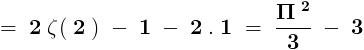
evaluate
1) \sum_{n=1}^{\infty }\frac{1}{n^3(n+1)^3}
2) \sum_{n=1}^{\infty }\frac{1}{n^2(n+1)^2}
these sums that u r giving require higher calculus as they cannot be done using trivial methods like telescoping
No brother ...why do u think so ;)
i wudnt hav given this if i wudnt hav seen this here in this thread
http://www.targetiit.com/iit-jee-forum/posts/practice-16277.html
post 18
if u can talk abt reimann zeta function here than u can very well solve this.
hmm ya may be MR.Ricky is well versed with the all these ,,
ok
i must have said "for iit aspirants "
its out of their range
again i wud say u r overestimating the prob
it doesnt hav something so fancy.
2
\frac{\pi ^2}{3}- 3
ricky may haven infinte methods methods for dis
I too was thinking of splitting by partial fractions...but can this be done without Riemann Zeta functions?
@ pritish
\zeta (2)=\sum_{n=1}^{\infty}{\frac{1}{n^2}}=\frac{\pi^2}{6}
take it as a fact
Well , this is directed to Nishant sir --
Nishant sir , once you asked , in the thread that asked to prove that the Harmonic series is divergent ( started by Subhomoy ) , that
summation of 1n 3 / 2 uptil infinity is convergent or divergent ?
But for any P - series , I mean , any zeta function having exponent greater than 1 has to converge to a finite value , shouldn't it ?? So the series is convergent .
yes you are right.. but then we were trying to prove that by some rule... which rule wud you use here?