but mavarick hasn't written anything abt equal or distinct roots --- otherwise my answer is same as yours
(1) Find all Integer a for which The equation x^{3}-13x+a=0 has three Integer Roots.
-
UP 0 DOWN 0 0 8

8 Answers
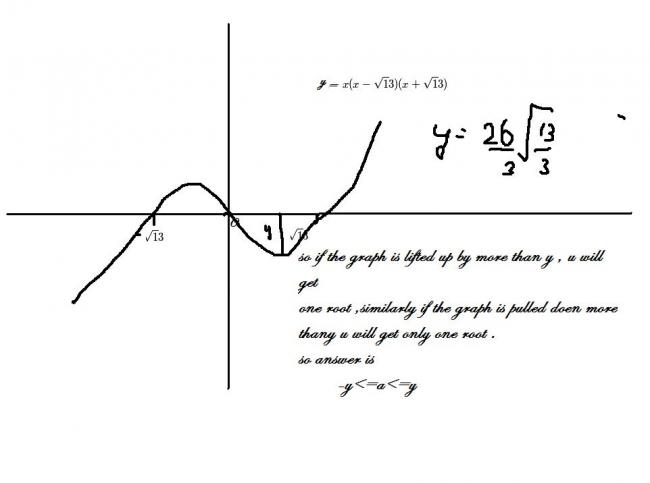
For a cubic to have 3 distinct roots, we must have f'(x)=0 for 2 values of x, say a and b, also f(a).f(b)<0
From which we have -12<a<12....
actually I don,t have answer for that question.....
so you may take both condition means equal roots and distinct roots.
If you take both the conditions , then a can take any value according to what x is , because you will always get an integer a such that
x^3 - 13x = -a.
Put x = 10 , we get 103 - 130 + a = 0 [ if we say that it has 3 solutions ]
Or a = -870
If we put a = -870 in x3 - 13x + a = 0 , then we get 3 equal
solutions 10 , 10 , 10 .
But by your graph this solution is not possible.
akari your graph is very much correct..
what is needed is integer roots..
so all integers satisfying your inequality.