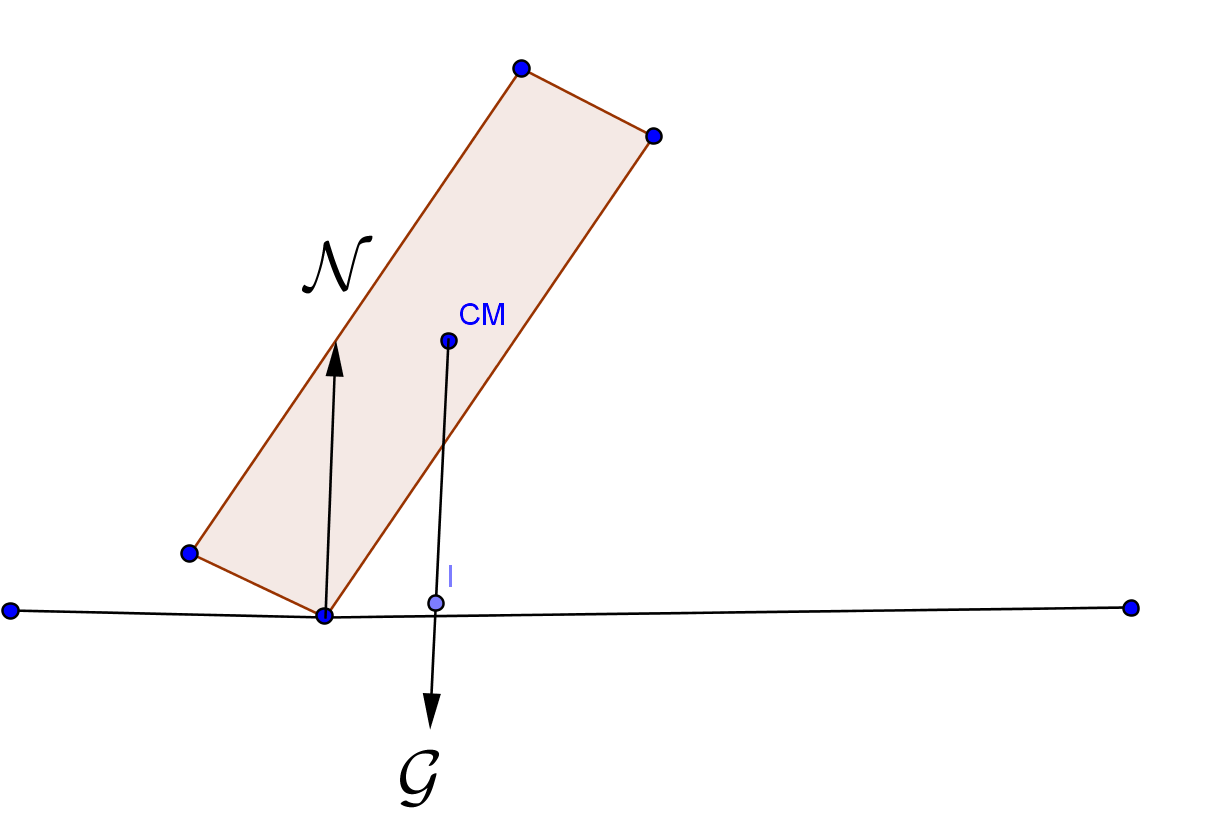
The figure gives us a cross-section of the coin as it falls.As you can see in the above figure,when the coin falls-
(1)There will be a gravitational force \mathcal{G} acting downwards and passing through the centre of mass(CM).
(2)There will be a normal force \mathcal{N}.
The above diagram is a random case.The torque about the point on the surface through which \mathcal{N} passes is clockwise.Hence it will topple.
Let us consider the following limiting case: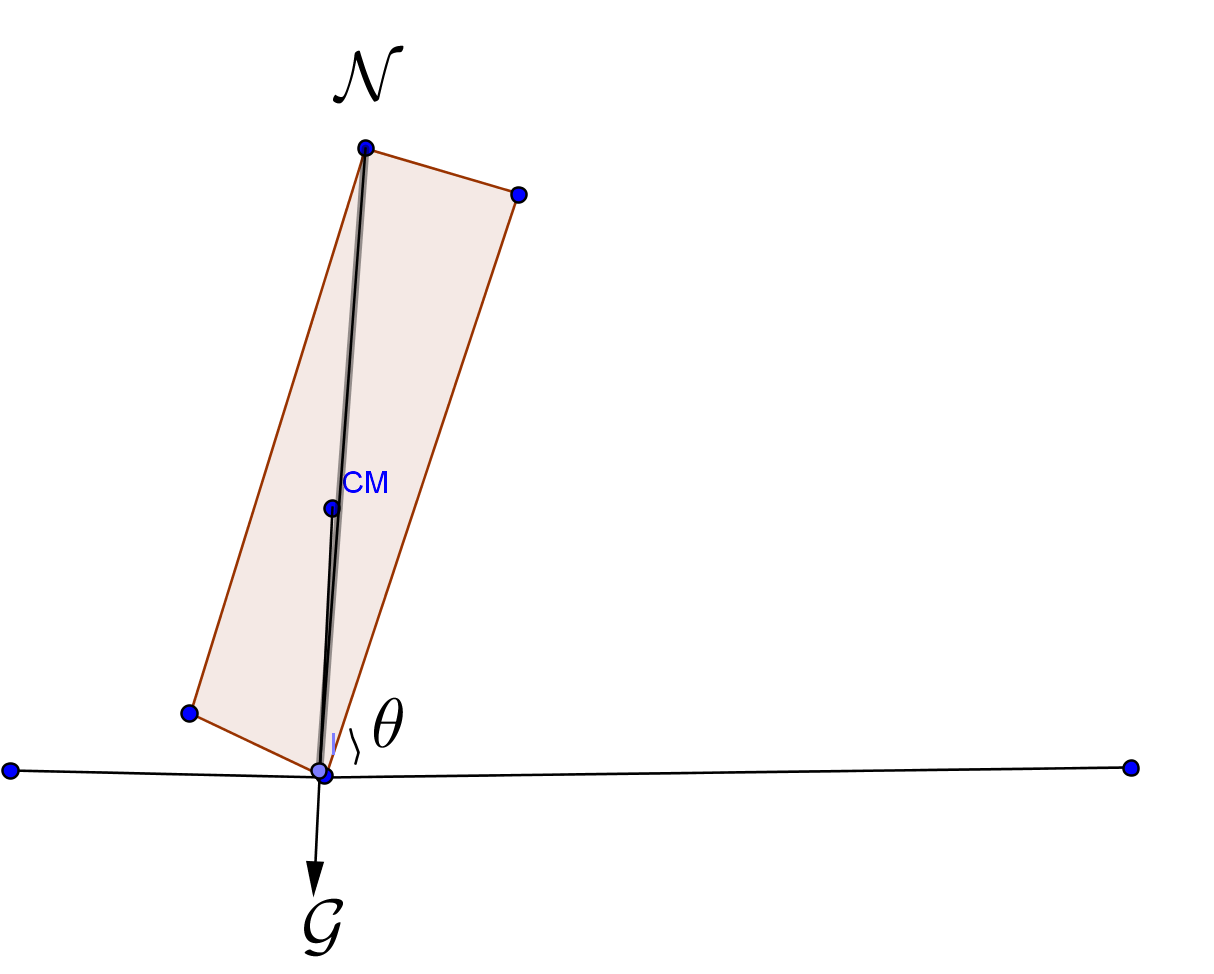
If the angle is greater than θ then it will not topple,otherwise it will.
So if the limiting case is θ the probability that it will stand =
All angles greater than θAll possible angles=θ90°
Here probability = 90°-θ90°= 13
or,θ = 60°
From the above diagram we can find tan(θ)= length of coin (i.e diameter)base(i.e thickness) = 2rbase= tan(60°)=√3
or, base = 2r√3