1sir is the ans correct
some of my friends are confused with percom so i want all here help them out with theory and problems alike......some are starting now...can nishant bhaiya help???
-
UP 0 DOWN 0 1 52
52 Answers
1Another of Nishant Sir's fav. monologues : " I do not believe in the proverb : common Sense is not so common !!! "
1no of ways of going from a to b then b to c=4*3=12as there are 4 ways from a to b and 3 from b to c.
no of ways of going from a to c directly=1
total no of ways=12+1=13
62lol...
no they are not copyrighted :P
one has been taken from another teacher of mine "common sense is not common"
while the perm comb one is my own ;)
62now another one..
what is the number of ways to go from A to B and then back to A if you
a) Dont use the same route again
b) Use the exactly same route again
c) Dont use any part of the route that he has taken once....
1ans to a) if one goes directly he cant use the same root back.if one goes back from c to b using one root he has three other choices left excluding one which he used while going so no of ways of returning=3*3=9.and for the direct route 3*4 ways are open for returning. so total no of ways =12+9=21
49my first sum which is also nishant bhaiya's favourite sum....here it goes....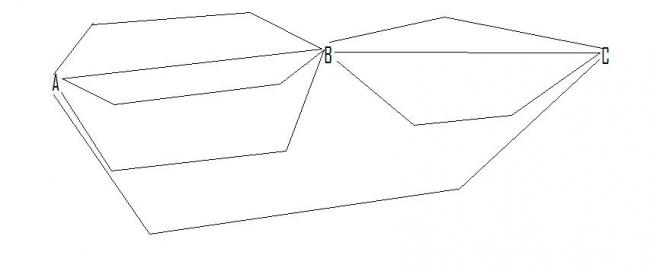
we have to find no of ways to go from a to c.......this is the easiest sum of all......so every will do it...
1amritansh ,nishant sir has already said that a)4*3 and b)4 are wrong read the whole thread
1Gosh every POST that ATGS starts continues like hot cakes !!!!!
49@LIGHT: do not be dukhi to hear this but i am still getting 87 for my ans...
49PROBLEM NO 2
Do this problem without using any formula
a)how many 3 digit nos can be made from 1,2,3,4,5,6,7,8,9???
b) " " " " " " " " " 1,2,3,4,5,6,7,8,9,0??
c)in a party there are 80 people. each people shakes hand with other people. how many hand shakes are there??
***do without formula.
i would love if Mr. LIGHT solve these....[1][1][1][1]
- Ayush Lodha 9 factorial*3factorial.
Upvote·0· Reply ·2013-02-10 02:53:43
- Ayush Lodha no the answer for the first will be 9c3 as we have to find the no of ways of the 3 digit so 9 nos will have 9c3 ways .
49well some1 asked for a high voltage sum....so here it goes...
listen to this story or donot as u wish but do the sum...
There were 5 iitans....they were really good friends....they had their first semester exams which was to continue for a week...they had planned to cheat in exam from each other and then enjoy by going to a film after the exam...due to cheating plans none had studied and every one gave really GREAT exam and so were angryon each other...one boy wanted to teach his frnds a lesson 4 nt studying so he bought 5 tickets to the FLOPPEST film ever..
as usual the hall was empty saving the 5 iitans....and no one was ready to sit beside each other...so,
FIND THE NO OF WAYS TO SEAT 5 IITANS IN A ROW OF 20 SEATS SUCH THAT NO ONE SITS BESIDE ONE OF THE OTHER ONES.........
I give the faltuest hint ever....u can do this by 2 methods one is a gadha ghora method and another a good easy method....try both...
i'll solve this first and give the answer in my next post....hidden tho....