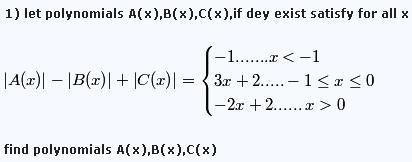341Seems to me that we cannot find such polynomials.
We will use the fact that for sufficiently large magnitudes of x, the sign of P(x) coincides with the sign of the leading coefficient.
For convenience I will write A instead of A(x).
Let G = |A|-|B|+|C|
There are two cases to be considered:
I. A and C have the same signs for the leading coefficient.
Then we see that G(x) = -G(-x) for sufficiently large magnitudes of x and this implies that |G(x)| = |G(-x)|
But we get a contradiction here as x \rightarrow \infty \Rightarrow |G(x)| \rightarrow \infty and x \rightarrow -\infty \Rightarrow |G(x)|=1
2. WLOG A and B have the same sign and leading coeff of C is -ve
Then we get the equations
A-B-C = -2x+2
-A+B+C = -1
which are true for infinitely many values of x
so that C ≡ x + 3/2 contradicting that leading coefficient of C is -ve
So no such polynomials A,B, C exist
1\\ \texttt{sir\: i\: dunno\: but \:ans\: given\: is\:\\ }\\ A(x)=\frac{3x+3}{2}\\ B(x)=5x/2\\ C(x)=-x +\frac{1}{2} \\
[12]
341
Hari Shankar
·2010-02-05 07:35:16
If you take A,B, C as given by you, then for x> 1/2, you get |A(x)| = A(x), |B(x)| = B(x) and |C(x)| = x - 1/2
So, |A(x)|-|B(x)| + |C(x)| = 1. So the answer provided by you doesnt fulfil the conditions.
1
Che
·2010-02-05 09:51:06
hmm
i guess u r rit
then may be ans given is wrong !
62ONe more observation, which i would like to put forward is this..
The nature of the function changes at the point where |A| or |B| or |C| is zero
so we should definitely have 0 and 1 as the roots of a few of the given polynomials.....
and the other roots should appear in multiples (if at all!)
And that gives more reason for the given answer to be incorrect...
1
Che
·2010-02-13 06:34:17
this prob actually has a printing mistake :P
its shud be jus C(x) instead of mod(C(x))
got to know today that it is a PUTNAM 1999 prob
i picked it from maths today.....and as usual it had a printing mistake....
i wont rely on maths today from now [16]
check this http://www.math.hawaii.edu/home/putnam/1999.pdf
