1ohh...yes!!!!
after reading ur reply to second question...i m sure to fail in interviews not to realise the obvious[2](thank god never faced one yet!)
doubt-1: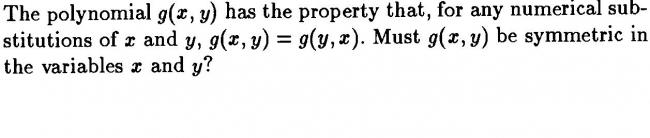
doubt-2: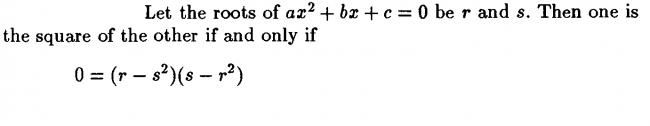
in this second doubt i can't understand how we came up with the condition to be satisfied for one root to be sqaure of other?
-
UP 0 DOWN 0 0 3
3 Answers
62if one is the square of other then it is easy that either r=s^2 or s=r^2
hence either (r-s^2) or (s-r)^2 is zero
hence their product is zero..
This condition can be exploited beautifully for a lot of such questions...
62First one seems to be correct.. but i will have to think of a formal proof
one method is to divide by highest power of y and take the limit y-> infinity... and keep x at 0
So the reverse value should also be equal (reverse i mean interchange of x and y)
this will lead to saying that the highest coeff of y has equal terms both in terms of x and in terms of constant term...
Use induction after that to complete the proof...
1