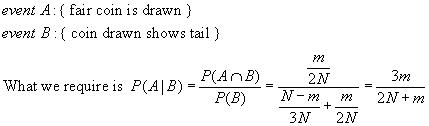THE OPTIONS R
(A)5
(B)6
(C)7
(D)8
Here i will be posting ques on probability which could prove to be useful 4 every1
Do try to give explanations if u can
options will be given on demand[1]
Q1
If the papers of 4 students can be checked by any one of 7 teachers , then the probability that all the 4 papers r checked by exactly 2 teachers
-
UP 0 DOWN 0 0 80

80 Answers
@tapan post #60
but u said answer is A ie 5 na ..................
Q4
A box contains N coins,of which m r fair and the rest r biased .The probability of getting head when a fair coin is tossed is 1/2 ,while it is 2/3 when a biased coin is tossed .A coin is drawn from the box it shows tail .The probability that the coin drawn is fair is........
COZ if the relation x<y doesnot exist then our ans wud easily double up and come down to "8" wich is a part of the options
yup the ques is perfect
mere ko sir ne orally bataya bhi tha
par main bhool gaya[2]
dhundhni padegi........
but thats the closest.......
pl. chk all ur specifications abt x,y are crrct in regard to x<y especially
x = 2007y/(y-2007)
now let y be 2007 + p coz x cant b negative
then x = 2007 + 20072/p
now chk diff values
yaar i dont have the answer to this 1
please post ur explanation!!!!!!!!!!!!!!!!
second :
y = 2007*10
x = 2007*10/9
3rd :
y = 2007*2008
x = 2008
4th :
y = 2007*224
x = 2007*224/223
tell me agar sahi aa rahe hai!
to i'll post more values
First :
y = 2007*4
x = 2007*4/3
MANI : [16] [16]
I TOLD Naa BHAI for Q1 it had to b wat I said ther was no oder Option [16]
neways chalta hai no probs [1] [4]
i appreciate ur work MR.MOHD [1]
NOW
Q3
The positive integer pairs (x,y)such that 1/x+1/y=1/2007,x<y,is???
no yaar ur absolutely correct...........i have posted my answer above but u gave the solution nice work........gud job.....(i dont knw ur name)...........
for d product to b divisible by 3, atleast one of d two no.s must b divisible by 3...
>> let first no. b 3 .... second one can b any of d remaining 99 no.s.... hence total no. of selections possible = 99
>> let first no. b 6 .... second one can b any of d remaining 99 no.s... but since (3,6) is already considered in first case, hence no. of selections here = 98
>> first no. = 9 .... total selections possible = 97
.
.
.
.
>> first no. = 99 .... total selections possible = 67
hence probability = 67+68+...+99 / 100c2
= 83/150...
most informal method, but still... easy approach...!!![3]
let me know if i'm wrong anywhr...!!!
hey manipal is the answer C)------>83/150.........plzz correct me if im wrong.........
ABHI BHAI
PERFECT ANSWER
PLEASE GIVE THE PROCEDURE TO SOLVE THIS PROBLEM
I AM GLAD THAT AT LEAST U TRIED[1]
Comprehension - 1
A class consists of n students. For 0 ≤ k ≤ n, let Ek denote the event that exactly k student out of n pass in examination. Let P(Ek) = pk and let A denote the event that a student X selected at random pass in the examination.
11. If P(Ek) = C for 0 ≤ k ≤ n, then P(A) equals
(A) 1/2 (B) 2/3 (C) 1/6 (D) 1/(n+1)
12. If P(Ek) = C for 0 ≤ k ≤ n, then the probability that X is the only student to pass the examination is
(A) 3/4n (B) 2/(n+1)
(C) 2/n(n+1) (D) 3/n(n+1)
13. If P(Ek) k for 0 ≤ k ≤ n, then P(A) equals
(A)3n/(4n+1) (B)3n+1/3n
(C) 1/n+1 (D) 1/n2
14. If P(Ek) k for 0 ≤ k ≤ n, then the probability that X is the only student to pass the examination is
(A)3/n(n+1) (B) 6/n(n+1)(2n+1)
(C)1/n (D) 1/n(2n+1)
PERFECT BHAI
MEKO PROBABILITY MEIN BAHUT TARAKI HAI
CHAL BAAD MEIN AUR QUES POST KAROONGA
after picking up one ball
remaining balls of favourable choice
n-1 of same colour
2 balls of other colour but the same no.
balls remaining 3n-1
req. probab
(n-1+2)/3n-1
http://targetiit.com/iit_jee_forum/posts/li_l_challenge_5_3951.html
check dis one...simillar Q
x1+x2+...+xk=n - k/2*(k+1)
M=n-k/2*(k+1)+k-1=n-k/2*(k-1)+k-1
bhai yeh thoda bhari ho raha hai
please explain kar do ki
1st step mein -k/2 X (k+1) kyun kia hai
aur 2nd step mein kya kia hai
sorry 4 this silly ques
i know i am a spoil sport
MCk-1 is the no. of integral solutions of
x1+x2+...+xk=n - k/2*(k+1)
M=n-k/2*(k+1)+k-1=n-k/2*(k-1)+k-1