13[11][11]
can it be 1/4
prob that length of a randomly chosen chord of circle lies b/w 1/2 and 3/4 of its diameter????
-
UP 0 DOWN 0 0 14
14 Answers
62we had done a big question on this one..
there are 3 ways to do this..
all will give different answers!
62http://targetiit.com/iit_jee_forum/posts/13th_december_2008_959.html
62@tapan: read the link I send before..
This is a very famous paradox.
If you can understand this at this stage it will be awesome..
21k k.. sure!!!
Sir, can u pl. tell me if the method of calculation I posted is crrct or not!!!
The area of the shaded portion can b easily found out by using definite integration as follows :
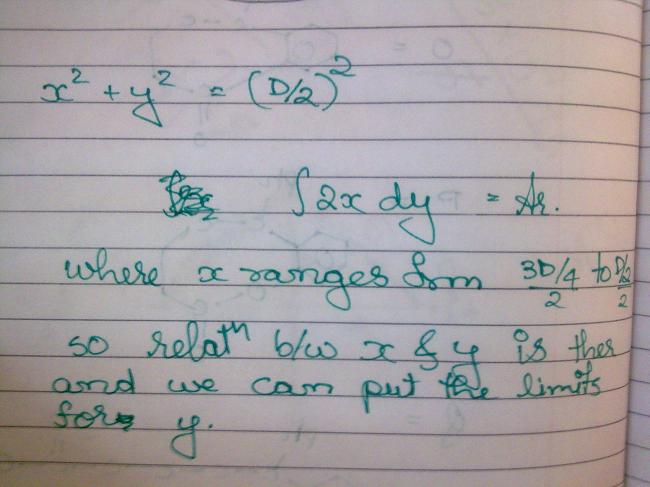
62tapan there is nothing wrong in your solution.. Just that there is a basic assumption of "what is uniformly random" that you have taken without realising it!
@eureka.. this question is not in syllabus.
Definitely Not.
If you are interested read the link I provided above.
At your stage many of you might not understand that. And it is not needed too!
21basic assumption of "what is uniformly random" that you have taken without realising it!
I din get dis, mayb i'll after digesting ur 3 proofs....
and meri method se sahi ans aega kya??
62actually yes and no...
Yes in a layman's language. But If I become a little "technical".. then Answer is No
21oh k... LOL....
I got the first proof, now processing proof 2 & 3.... [12] [7] [12] [7] [12] ........
21now i feel my meth is RONG as it takes into account length of the chord which shudnt b da case..........
11A variation of this one
The probability that the length of a randomly chosen chord of a circle is between 1/2 and 4/5 of the diameter is
62tapan, your method is not wrong.. there is something intrinsic that has to do with the fat that this is a continuous case...