If lzl=1 ,prove that the points represented by \sqrt{\frac{1+z}{1-z}} lie on one or the other of two fixed perpendicular lines
62This was proved sometime back on the forum... i dont remember the link...
62here is the link
[url=http://www.targetiit.com/iit-jee-forum/posts/complex-geometry-295.html]Complex numbers...[/url]
66Let
x=\sqrt{\dfrac{1+z}{1-z}}
Then, x^2=\dfrac{1+z}{1-z}
Or
z=\dfrac{x^2-1}{x^2+1}
Since |z|=1, we get
|x^2-1|=|x^2+1|
That is x2 lies on the imaginary axis. So, x itself lies either on the line through the origin inclined to the real axis at 45° or 135°.
3
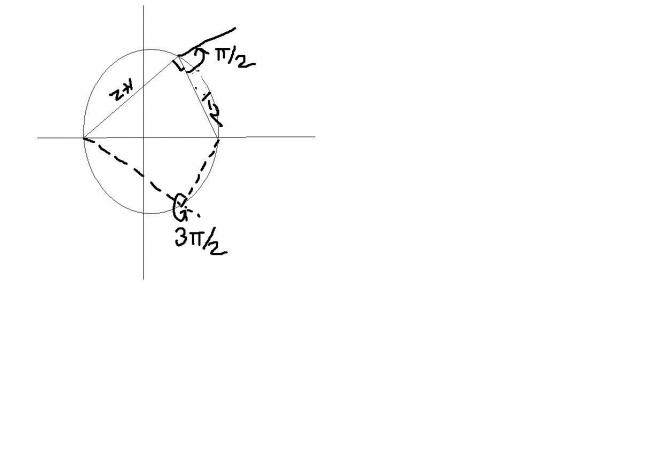
a nice way of lookin at it is through geometry see the figure and use the concept of rotation :))
62wow that is a great one..
one cant describe how stupid my solution looks in from of this one :D :P