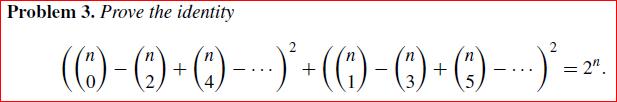Prove the identity

\bf(1+x)^n=C_{0}+C_{1}x+C_{2}x^2+C_{3}x^3+C_{4}x^4....................$\\\\ Put $\bf x=i$, We Get\\\\ $\bf (1+i)^n=C_{0}+C_{1}.i+C_{2}.i^2+C_{3}.i^3+C_{4}.i^4................$\\\\ $\bf (1+i)^n=C_{0}+C_{1}.i-C_{2}-C_{3}i+C_{4}.........................$\\\\ $\bf (\sqrt{2})^n.\left(cos\frac{\pi}{4}+i.sin\frac{\pi}{4}\right)=C_{0}+C_{1}.i-C_{2}-C_{3}i+C_{4}.........................$\\\\ Equating Real and Imaginary Part,We Get\\\\ $\bf C_{0}-C_{2}+C_{4}.........=(\sqrt{2})^n.cos\frac{\pi}{4}$\\\\ $\bf C_{1}-C_{3}+C_{5}.........=(\sqrt{2})^n.sin\frac{\pi}{4}$\\\\ Squaring and Adding, We Get\\\\ $\boxed{\boxed{\bf \left(C_{0}-C_{2}+C_{4}.........\right)^2+\left(C_{1}-C_{3}+C_{5}.........\right)^2=2^n}}$

Wah!! Thanks!