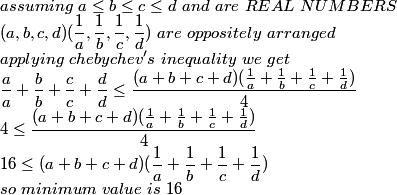
7 Answers
no . try the Am Hm inequality , we get 16 , as the min value.
or , the rule.
I dunno . waht it's called . plugging in a=b=c=d=1 . we get the min as 16 .
It's some theorem . I dunno . the min occurs at ±1 .
Better not confuse you . ask Nishant or Abhishek. they'll know better.
i m nt with dat +- like thng as its value is 16 for all 2n like numbers
bt yup i made a mistake ans is 16
Try AM≥HM here
(a+b+c+d)/4≥4/(1/a +1/b +1/c +1/d)
(a+b+c+d)(1/a +1/b +1/c +1/d)≥16
so minimum value is 16
or, by cauchy schwarz inequility,
(a/a+b/b+c/c+d/d)2≤(a+b+c+d)(1/a+1/b+1/c+1/d)
=> (a+b+c+d)(1/a+1/b+1/c+1/d) ≥ 16
so the minimum value is 16
Since the question is symmetric in a,b,c,d so min occurs at a=b=c=d...
As why you will give preference to any one of them (others will get angry..)
this method is quite helpful in objectives but not so dependenable....