11
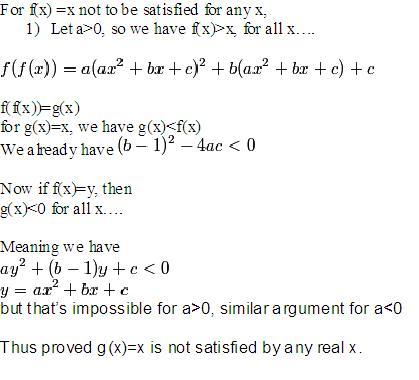
This was posted in another iitian forum (by one of our members :D). Its a nice problem so I flicked it.
Let f(x) = ax2+bx+c be such that the equation f(x) = x has non-real roots.
Prove that this implies that the equation f(f(x)) = x too has non-real roots
-
UP 0 DOWN 0 1 3
3 Answers
341thats correct.
There's a simpler method though.
As you rightly observed, f(x) = x does not have real roots implies f(x)>x for all real x or f(x)<x for all real x.
We will just look at f(x)>x as the same reasoning holds for the other case too.
We have f(f(x))>f(x)>x for all real x and hence the equation f(f(x)) =x has no real roots
finis!