Ans 2) f(x) = A0 + 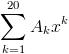
= 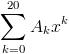
= 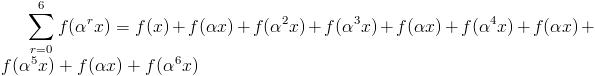
= 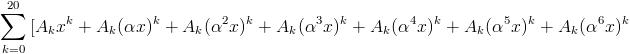
= 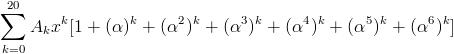
= 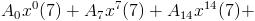 [bcoz sum of 7, 7th roots of unity = 0 ]
[bcoz sum of 7, 7th roots of unity = 0 ]
= 7 (A 0 + A7 x 7 + A14 x 14 )
Thus, k = 7
i need the best and shortest methods to solve these in exma hall...
Q1 Let P(x)=x^5+x^2+1 have roots x_1,x_2,x_3,x_4,x_5
and g(x)=x^2-2
then find value of g(x_1)g(x_2)g(x_3)g(x_4)g(x_5)-30g(x_1x_2x_3x_4x_5)
Q2 Let \alpha =e^{i2 \pi /7} and f(x)=A_0+\sum_{k=1}^{20}{A_kx^k} and value of f(x)+f(\alpha x)+f(\alpha ^2x)+...f(\alpha ^6x) \ is \ k(A_0+A_7x^7+A_{14}x^{14}).Find k
Q3 f:R\rightarrow R \ is \ f(x)=ln(x+\sqrt{x^2+1})
the find no. of solns to eqn \left| f^{-1}(x)\right| =e^{-\left|x \right|}
Ans 2) f(x) = A0 + 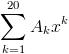
= 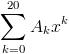
= 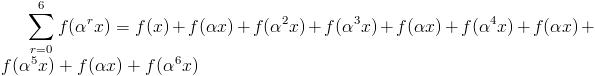
= 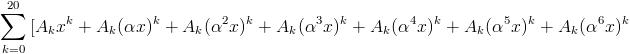
= 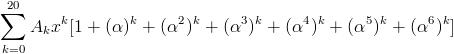
= 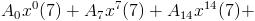 [bcoz sum of 7, 7th roots of unity = 0 ]
[bcoz sum of 7, 7th roots of unity = 0 ]
= 7 (A 0 + A7 x 7 + A14 x 14 )
Thus, k = 7
i guess that there is no short method possible,i guess u know the soln :P,infact we were given two solns for qn 1.
i ques 2..since the equation holds true for any x, it will also be true for x=0
this directly gives k=7
But Q1 is quite straightforward. They are just asking for P(\sqrt 2) P(-\sqrt 2) - 30 g(-1)
@prophet Sir how did u get P(√2).P(-√2) ??
@ bipin bhaiya ....thx
@tush , thx
@msp....BT solns are more complicated than their ques....thats why i asked here....moreover both the solns they gave were useless..
y=ln(\sqrt{x^2+1}+x)
\sqrt{x^2+1}+x=e^y
so,\sqrt{x^2+1}-x=e^{-y}
from these two : x=\frac{e^{y}-e^{-y}}{2}
f^{-1}(x)=\frac{e^{x}-e^{-x}}{2}
so, \left|\frac{e^{x}-e^{-x}}{2} \right|=e^{-|x|}
when x<0 : \frac{e^{-x}-e^{x}}{2}=e^{x}
\Rightarrow x=-\frac{ln3}{2}
when x>0 : \frac{e^{x}-e^{-x}}{2}=e^{-x}
\Rightarrow x=\frac{ln3}{2}
Eureka - isn't it obvious for q1)?
\prod_{i=1}^{5}{g(x_i)}}=\prod_{i=1}^{5}{(x_i\pm \sqrt{2})}
P(x)= \prod_{i=1}^{5}{(x-x_i)}
Substituting x=\sqrt{2}, we have \boxed{ \prod_{i=1}^{5}{g(x_i)}=P(\sqrt{2})P(-\sqrt{2}) }.