115) Is x≠y?
1) Find all natural n's for which n4 + 2n3 + 2n2 + 2n + 1 is a perfect square.
2) If [a] is the grestest integer not exceeding a and a = 2 + √3 then the value of an + a-n + [an] for any positive integer n is
3) Find the number of integers α for which the equation x3-13x+α=0 has integer roots
4) Find the perimeter of the octagon formed by the roots of the polynomial equation z8-256=0 plotted in the complex plane in order.
5) Find all integers (x,y) satisfying x+y=x2-xy+y2
-
UP 0 DOWN 0 0 11
11 Answers
111)the equation simplifies to (n+1)2(n2+1)
For the above equation to be a perfect square n2+1 has to be a square. But we know that n2+1 is not a square for any natural no. Thus, there are no natural no.s for which n4 + 2n3 + 2n2 + 2n + 1 is a perfect square.
215) I am a fool . :(
after quite some time i realized this is easy
This is just (x-y)2+ (x-1)2+ (y-1)2= 2
Solutions are easy to find out now.
@sambit: Nice solution to 1. [1]
341for 1 if the factorisation does not occur to you (as it did not to yours truly), you can write it as:
(n^2+n+1)^2+n^2
and we have
(n^2+n+1)^2<(n^2+n+1)^2+n^2<(n^2+n+1)^2+2(n^2+n+1)+1=(n^2+n+2)^2
So the given expression lies between two consecutive perfect squares and so cannot be a perfect square
341For 3: i think you mean all three integers. Otherwise if you take \alpha = 13n-n^3 for any integer n you are done.
If more than one root is an integer. Then let the roots be a,b and c with a≥b≥c
So a+b+c = 0 and ab+bc+ca= -13
i.e. a^2-bc = b^2-ca = c^2-ab = 13
so that (a-b)^2+(b-c)^2+(c-a)^2 = 78
The only solutions among integers are
a-b=2, a-c=7 and b-c =5 which gives a=3, b=1 and c=-4
So \alpha = -abc = 12
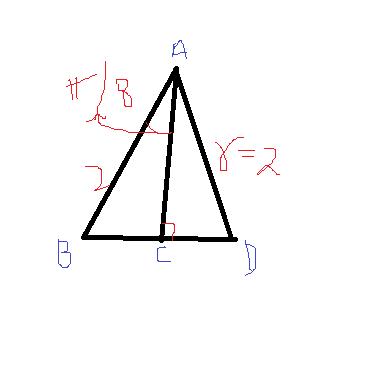
2624) 
z8 = 256 = 28
hence |z|=2
one section of the octagon is ABD.
in triangle ABC,
ang. BAC= 2pi/16= pi/8
AB=|z|=2
hence BC=2.sin (pi/8)
therefore perimeter= 16*2*sin(pi/8)
1@ Hari Shankar sir : For 2 i meant the same thing sir. And can u please tell why it is equal to 1? For 3 i did mean all three roots are integers.
@ Aditya : Can u please tell why ang.BAC=2pi/16
262@sri- for the whole polygon, total angle = 2pi
now for section ABD which is 1/8 of the whole polygon ang. ABD = 2pi/8
but ABD is isoceles.
hence ang.ABC=ang.CBD = 2pi/8 * 1/2 = 2pi/16
1@ Aditya : I think u mean ang. BAD=2pi/8. And how did u get ang.CBD=2pi/8 ????
Please correct your post. And thank you for your help.