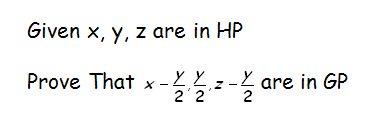Sequence And Series Interesting Question. Need Solution

Ok.

Given that x,y,z are in H.P.

=> \frac{1}{x},\frac{1}{y},\frac{1}{z} are in AP

=>2\frac{1}{y}=\frac{1}{x}+\frac{1}{z}

Multiply both sides by xyz and a bit rearrange

=>xz = \frac{xy}{2}+\frac{zy}{2}

Take the terms on RHS to left side and Add both sides \frac{y^{2}}{4}

=> Take common and you have \frac{y^{2}}{4} = (x-\frac{y}{2})(z-\frac{y}{2})

Hence, the result

One more...!!

x,y,z are in H.P

so, y = 2xz/(x + z)

=> xy + yz = 2xz
=> yz = 2xz - xy
=> yz = x(2z - y)
=> 2yz = 2x(2z - y)
=> 2yz - (2z - y).y = 2x(2z - y) - (2z - y).y
=> 2yz - 2yz + y² = (2z - y)(2x - y)
=> y² = (2z - y)(2x - y)
=> y²/4 = (2z - y)(2x - y)/4
=> (y/2)² = (z - y/2)(x - y/2)
=> x - y/2, y/2, z - y/2 are in G.P [by the def. of G.P]