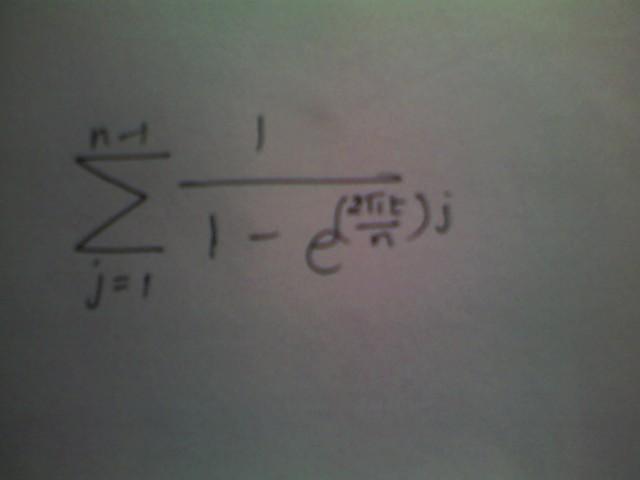i think it will convert to a g.p
12 Answers
Use 11-x=1+x+x2+......then separate the real and img parts....ans shud be (n-1)/2 if I've not made calculation mistakes.
A much simpler method would be
s=\sum{\frac{1}{1-z}}=\sum{\frac{1}{1-1/z}}
The above statement holds because the numbers are complex roots of unity
Hence on adding the two, \\2s=\sum{\frac{1}{1-z}}+\sum{\frac{1}{1-1/z}} \\2s=\sum{\frac{1}{1-z}}-\sum{\frac{z}{1-z}}=\sum{1}
Thus, s=(n-1)/2 (Edited)
(I am sure some of you.. specially the beginners must not have understood what i have written.. just try to read a couple of times and you are done...
Interesting enough, but I don't see any i (the imaginary unit) appearing in the sum, yet people are talking about complex number. I read the question as
\sum_{j=1}^{n-1} \dfrac{1}{1-e^{(2\pi t/n)j}}
Is that so?
yes Kaymant sir
I also don't see the iota in the summation so i asked him to write the exponent term clearly
\sum_{j=1}^{n-1}{\left(\frac{1}{1-e^{\frac{2\pi ij}{n}} \right)}
And nishant sir, check ur ans - i thnk it's wrong.
yes raja..
and yes kaymant sir.. i solved it by what raja has written.. otherwise, obviously the sum does not seem to be valued at (n-1)/2
nishant bhaiyya..... derz no i in d ques....no complex no. at all....it is (2Î tn) j