2305
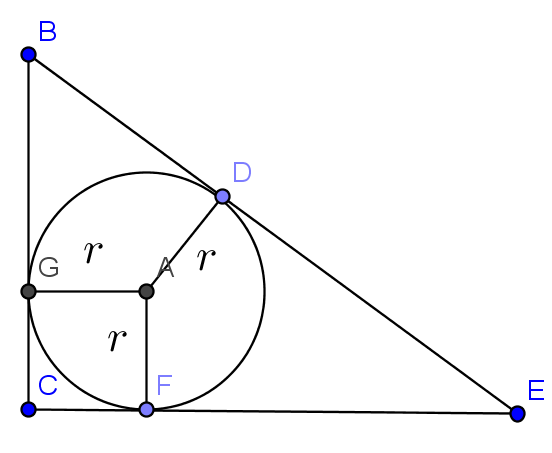
\text{Area of }\Delta BCE = \Delta BAC+\Delta CAE+\Delta BAE
\text{Let }BC =x,CE=y,BE=z
\frac{1}{2}xy=\frac{1}{2}rx+\frac{1}{2}ry+\frac{1}{2}rz
\frac{x+y+z}{xy}=\frac{1}{r}=\frac{1}{2013}
\text{It's known that if gcd(x,y,z)=d and x,y,z are a pythagorean triplet then }
x=d(2st),y=d(s^{2}-t^{2})\text{ and }z=d(s^{2}+t^{2})\text{ where }s,t>0
\text{Using this we get }\frac{1}{d \cdot t(s-t)}=\frac{1}{2013}
\text{or, }d\cdott(s-t)=2013
\text{So I guess the answer is (c)27.(Tell me if I am wrong)}
1133how do you solve dt(s-t) = 2013?
2305
Shaswata Roy
·2013-03-14 09:05:57
2013 = 3\times 11\times 61
\text{We form a ternary number(a number of base 3)}
\text{If a digit contains 0 then the corresponding number goes to (s-t),}\\\text{if 1 then the corresponding number goes to t,}\\\text{and if 2 then the corresponding number goes to d,}
\text{For example}
\text{1)We consider the number 210.So 3 goes to d,}
\text{11 goes to t and 61 goes to (s-t)}
\therefore d=3,t=11,(s-t)=61\text{ or }s=72
\text{2)Let us consider the number 221 .So 3 goes to d,11 also goes to d,61 goes to t}
\therefore d=33,t=61
\text{We are left with s-t which is obviously}=\frac{2013}{d\cdot t}=2013/2013=1\\\text{ or } s=62
\text{No. of ways to form such a no. = }3\times 3\times 3=27
(\because\text{there are 3 ways to fill in each of the digits of the ternary no.(2,1 or 0))}
2305
Shaswata Roy
·2013-03-15 04:20:47
Basically d can have any of the 3 factors,t can have any of the factors and s-t can have any the 3 factors.So total no. of solutions for d*t*(s-t)=3x3x3=27
1357there is one another method you can try
let the sides be a+2013, b+2013, a+b
where a+b is the hypotenuse
using the formula r=(s-c)tan(C/2)
So we have
(2013+a)2+(2013+b)2=(a+b)2
2*20132=(a-2013)(b-2013)
total number of solution is 54
so we have to take half to avoid repetition
