Philip all the best da for tommorow....[1][1][1][1][1]....have u got any tension for the chemistry exam??......
This is the famous Tower of Brahma (Tower of Hanoi) problem where it is believed that when this whole thing is completed by priests the world will come to an end.
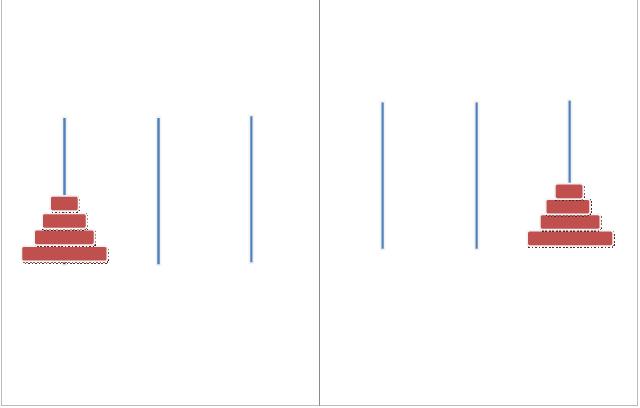
Arrangement: Threre 3 Rods. One containing N discs. In descending order of size.
Aim: to go from Arrangement on left to Arrangement on Right
Constraints:
1) At any stage a small disc cannot be below a larger disc
2) One disc is to be moved at a time
Prove: The minimum number of moves to achieve this change is 2n-1
Hint: Try using some recurrence relation!
There are 64 discs in the tower of brahma problem.
-
UP 0 DOWN 0 0 27

27 Answers
I THINK KUMAR DESERVES A PINK .... CUZ HE WAS THE FIRST 1 TO ANS. IT CORRECTLY!!!!
bahut zyada GUSSA aata hain tumhe mere dost!!!
CapitoLs or NO capitols dusnt make a diff 2 me!!!
BUT YA ur pt. regardin p and q is taken.... u hav got a point ther....
p,q shudnt be equal!!!
but ya how do u prove that this assumption can b safely made??
very strange kind of person you are tapan.........
jus see again have you put the value of f(x) correctly
and anyways
f(n) = 2f(n-1) + 1
==>
f(n) = 2^n - 1
so p and q can't be same anyway and plz dont use capitals everywhere.......
NO PHILIP!!!!
THOSE P's CAN VERY MUCH BE THE SAME.... RATHER IT WUD B A CASE OF ADJUSTIN IF U TAKE P AND Q DIFF. WHICH IS IS WRONG...........
f(n) = 3*f(n-1) + p;
f(x) = 3^x + p;
3^3 + p = 3*3^2 + p;
THE ABOVE EXPRESSION WUD NOT HOLD IF P AND Q WER DIFF!!! [12]
HOPE U GOT MY POINT!!!
tapan first of all be careful abt wat you are posting....
if f(n) = k*f(n-1) + p;
f(x) = k^x + p ???????
those "Ps" have to be diffnt...
if f(n) = k*f(n-1) + p;
then f(x) = k^x + q (assume)
so we have..
k^x + q = k(k^(x-1) +q) + p
so
k^x + q = k^x + kq+p
so kq + p = q..... knowing k and p we get q [1]
this is looking tidy....and can be done !![1][1] (unless k =1 which is a much easier case )
akand :
DUDE, c properly,
my statement says :
f(n) = k*f(n-1) + p;
f(x) = k^x + p
which wud imply if ur k=3;
f(x) = 3^x + p;
3^3 + p = 3*3^2 + p;
I guess u hav misinterpreted my statement!!!
Bhaiyya plzzz dont complete it..........dont answer plzzzz.I dont want d world 2 end....
I WANNA LIVE......waaaaahhh atleast till April 12th.....
well tapan i dont think so............coz lets take an example.....
let f(x)=x2 and let n=2 , k=3 and p=1....just imagine..
so f(n)=f(2)=4=k(f(n-1) +p
=kx1+p
= 3+1=4
but kn+p=k2+p=9+1=10 which is not 4........
hope this helps
GENERAL DOUBT :
WENEVER WE GET SUMTHING LIKE THIS :
f(n) = k*f(n-1) + p;
f(n) = k^n + p ??????? [7]
can we assume this or cud it b disastrous at times?
ok i'll give something else.......
to move n discs from source to dest......
move n-1(from top) to intermediate ....
then move the nth one to the dest........
and finally top that one with the n-1 discs from intermediate to dest..
that is what i and kumar have done.........
Philip all the best da for tommorow....[1][1][1][1][1]....have u got any tension for the chemistry exam??......
now i see Kumar has already done that...bhaiyya isn't that correct.
2n-1
first we need to break it into two parts......one part will b the base and rest is other part..
.....then recursing in this way gives ultimately the pair with only 2 discs which is esy to solve.......hope this is useful
btw a better question would be when one more peg is added ...
after all i havent as yet been able to that one...!!
let f(n) give the no. of moves reqd to shift n discs from the source peg to destination peg.....
then f(1) = 1
f(n) = f(n-1) + 1 + f(n-1)
or f(n) = 2f(n-1) + 1
this should be it...
now i think someone else who is not struggling with his boards like me has to take it from here....
sorry if the question is not what i think it is bcoz i haven't gone thru the whole of what bhaiyya has written i only saw"towers of hanoi and started typing [1]
Sir, I had don this as my std 10 project!!!
the formula for total moves was sumthing like 2^n blah blah... dont remember exactly!!!1
But ya I dont know how 2 provwe dat formula apart frm observation!!!
Do u expect us 2 work out the proof.... then i'll giv it a shot
hey no one proved this yet... why!!?
It is not as tough as it looks ;)
A c++ source code:
it shows stack status after every move...........
http://sites.google.com/site/priyamspage/Home/files
I think it is like this
T(n) = T(n-1) +1 + T(n-1)
T(n) = 1 + 2.T(n-1)
Now T(1) = 1 = 2-1
So T(2) = 2 + 1 = 4 -1
T(3) = 6 + 1 = 8 - 1
.......
.......
......
yes this is the same thing.. it is called both The tower of Hanoi and the Tower of Brahma.. And even I did it in C++ :D
@nishant,
hey this is sumthing i studied once in C++... with sum other name... sumthing like tower of hanoi or sumthing like that... (!)