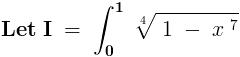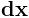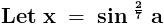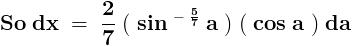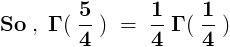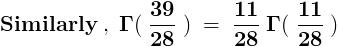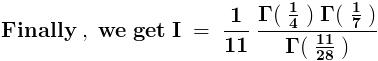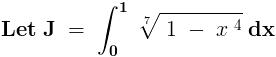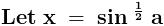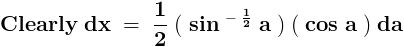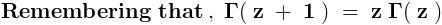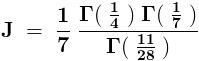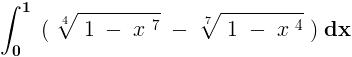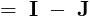Img not visible, Che.
.......................................................................................................................

-
UP 0 DOWN 0 0 9

9 Answers
wow man
i bet this guy isnt in 11 th or 12th
and ya ans is 0
but its much simpler .....both fuction r inverse of each oder....so ?
even i bet that once and lost :P
:D
Yeah that is the right way...
"They are inverse of each other"
Consider , 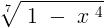
Domain - { - 1 , 1 }
Range - { 0 , 1 }
Now , consider the other integral , 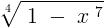
Domain - { - ∞ , 1 }
Range - { - ∞ , ∞ }
The domain of the inverse funtion should be equal to the range of the parent function and vice - versa ,
and this holds for any function having an inverse .
But , here that doesn't hold . So are these functions inverses of each other ?
No . Actually , the inverse of 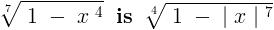 .
.
Hence , the argument given by Che is not correct .
Well....
fof-1(x) = x [My favourite property :P]
=> (1 - (f-1(x))4 )17 = |x|
=> 1 - (f-1(x))4 = |x|7
=> (1 - |x|7)1/4 = f-1(x)
I guess he has a point. This property must hold for all functions and their inverses, and for it to hold here x must be non-negative as the LHS is also non-negative.
@Ricky, if you restrict the domain then it is true that the functions are inverses of each other.
See http://www.goiit.com/posts/list/integration-sir-please-reply-67432.htm last method for some elaboration