2) Will there be 6 solutions??
1) let polynomials A(x),B(x),C(x),if dey exist satisfy for all x

find polynomials A(x),B(x),C(x)
2) Find all (x,y) such that
 .
.
-
UP 0 DOWN 0 1 16

16 Answers
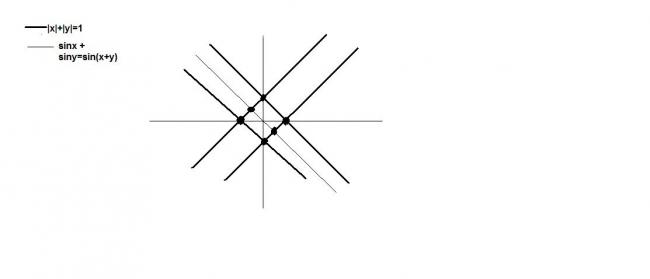
sinx + siny=sin(x+y) are the set of lines x=0, y=0, x+y=0. Plotting the graph alongwith that of |x|+|y|=1, 6 solutions are coming..draw the graphs and check it out
ok will try to find some non-graphical approach..if i get it, will post it
btw jus prove ur statement "sinx + siny=sin(x+y) are the set of lines x=0, y=0"
its from the concept of light rays...when we draw a light ray, we draw a straight line...thats from the macroscopic view...from the microscopic view, light rays are waves. they also have crests and troughs.
array i said na
i want a mathematical proof
not a proof inspired from a physics concept
2sin\frac{x+y}{2}cos\frac{x-y}{2}=2sin\frac{x+y}{2}cos\frac{x+y}{2}\\ \Rightarrow 2sin\frac{x+y}{2}sin\frac{x}{2}sin\frac{y}{2}=0 \\thus\:either\:sin\frac{x+y}{2}=0\Rightarrow x+y=2n\pi........i\\ \\ or\\sinx/2=0\Rightarrow x=2n\pi.....ii\\ or\\ siny/2=0\Rightarrow y=2n\pi....iii
got it................[1]
plz somone giv soln for 1