11can sum1 pls post the method or solution
No. of solutions of eqn.---
| Sin Ï€(pi)x/2 + Cos Ï€x/2|=√|(ln |x|)^3|+1
A. 4
B. 6
C. 8
D. none of these
-
UP 0 DOWN 0 0 16
16 Answers
1correct question is (its from fiitjee AITS )
|sin∩x/2 + cos∩x/2 | = √|(ln |x|)^3|+1 (whole sqrt)
1square both sides
=> [ln|x|]^3 + 1 = sin∩x + 1
=> [ln|x|]^3 = sin∩x
draw the graph of sin∩x and LHS
no. of solutions = 3+3=6
if u r facing problems in finding their intersection point ,do tell me, i will help :) .. pretty easy though
11can u pls show how it is 6.. wont it b 4 ?? it wud b nice if u cud post ur graph.. :)
1here is the original graph
directly plotting LHS and RHS as given in question
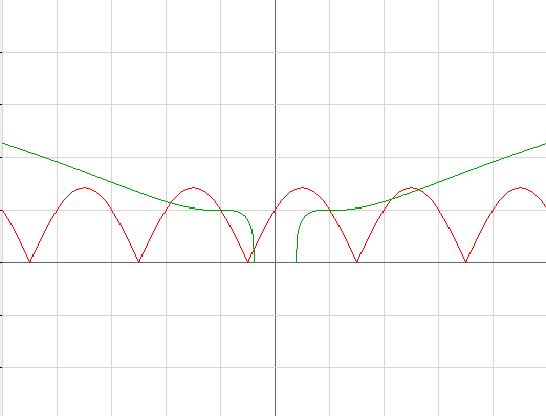
also visulalise that x coordinate of intersection is same in both the graphs..this is what i wanted to show u :) ..this is difficult to plot but i took the help of graph generator. first one is easy just keep chking the values of ln1,ln2,ln3..(there cube actually) and decide whether it will intersect the given branch of sinpi*x or not
