341you are right. I have edited it in the post now.
Let f'(sinx)<0 and f"(sinx)>0, for all x belonging to (0,pi/2) and g(x)=f(sinx)+f(cosx) then..
a) g(x) is increasing in x ε (0,pi/4)
b) g(x) is increasing in x ε (pi/4,pi/2)
c) g(x) decreases in (0,pi/4)
d) g(x) is increasing in x ε (0,pi/2)
(More than one correct..)
[7]
-
UP 0 DOWN 0 0 35
35 Answers
21case 2 mein dbt
how can u say this -A + B < 0
as cosx > sinx , then accordingly f(cosx) aur f(sinx) bhi to change hoga.... [7]
33Kuch kuch ho gaya..
f(cosx)<f(sin(x)) for 0,pi/4
f(sinx)<f(cos(x)) for pi/4,pi/2
21yeh priyam, that was precisely wat i was hintin at in #5 Posted
33huh!!
that was easy...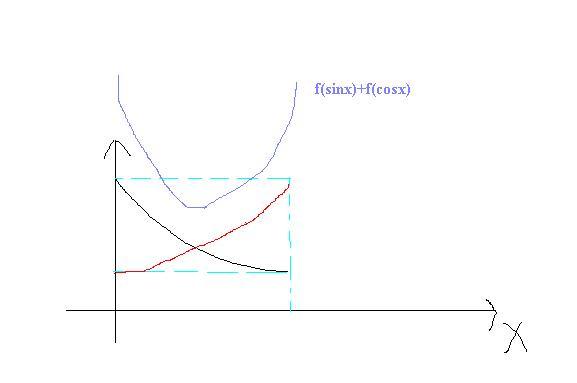
red is f(cosx)
black is f(sinx)
also g(x) is symmetric about pi/4
341g(x) = f(sin x) + f(cos x)
g'(x) = f'(sin x) cos x - f'(cos x) sin x
Let h(x) = f(sinx)
h'(x) = f'(sin x) cos x
h"(x) = -f'(sinx) sin x +f"(sin x) cos x>0 (from the given conditions)
That means the function H(x) = h'(x) = f'(sinx) cos x is an increasing function in x.
Now H(Ï€/2 -x) = f'(cos x) sin x
So g'(x) = H(x) - H(Ï€/2 -x)
When x ε [0, π/4), π/2 -x>x so that H(π/2 -x)>H(x) so that g'(x)<0 in this interval
In the same way g'(x)>0 in (π/4, π/2]
[edited typo pointed out by tapan]
21h'(x) = f'(sin x) cos x
h"(x) = -f'(x) sin x +f"(x) cos x>0
frm wer did the bold "x" come shud it not be sinx???
pl. forgive me if i am wrong
21OHKKKK.....
GOT IT!!! WAT A WONDERFUL SOLTN....
[1][1][1][1][1][1][1][1][1][1][1][1]
11Can we solve this ques this way.....??
g(x) = f(sin x) + f(cos x)
--> g '(x) = (cos x) f '(sin x) - (sin x) f '(cos x)
--> g ''(x) = - (sin x) f'(sin x) - (cos x) f '(cos x) + (cos2x) f ''(sin x) + (sin2x) f ''(cos x)
g(0) = g(pi/2) = f(0) + f(1)
Applying Rolle's Thrm,
for g '(c)=0 , we get c=pi/4
Also, g ''(pi/4) > 0. Therefore , we have minima at pi/4.
Thus we can say that
g(x) is decreasing in (0,pi/4)
& g(x) is increasing in (pi/4,pi/2)
21hmmmm ya I found no prob with this methhod..... nice way of thinkin!!![1]
62but how does this prove that there are no other maximas and minimas
21point!!
par agar g'(c) = 0 for only 1value of c b/w 0 to pi/2 then it wud mean that ther are no other max-min.....
21Sir, pl. correct me if i'm wrong.....
I wanted to get this prob solvin tekniqu of rish confirmed by you as I feel its a nice way of thinkin in this inc/dec.ing function type sums....
pl. help
341@rkrish: Not really. Having a minima at π/4, only tells us the behaviour of the function in a small neighbourhood of π/4.
We are asked to deduce a stronger result in the interval.
21LOL ....... [4] [4][4]
wen theprocessing finishes and if u get an output pl. mention!!!
the queston will be depndent on
f'(sinx)/f'(cosx) >/< = tanx
u gotta adjust the signs as per division by -ve no.....
I m still [12] [12]
39priyam see if this helps.............
if p(x) and q(x) are two functions and r(x)=p(x)+q(x)
then r(x) is incrasing only when both p and q are either increasing or decreasing
r(x) ia decreasing if one of them is decreasing and other is increasing
[sorry if u already knew this]
21thnx 4 da info!!
but over here it wud be a case like : r(x) = f(p(x)) + g(q(x));
so it wil cahnge na.... WAT SAY??
21are these observation correct?
f(x) is dec thruout its range.....
f'(x) is inc thruout its range.....
1g'(x) = cosx f'(sinx) - sinxf'(cosx)
f(cosx) = f(sin(Î /2-x)) [tx priyam [1]]
=> f'(sinx) = -f'(cosx)
=>f'(cosx) = -f'(sinx) >0
g'(x) = cosx f'(sinx) - sinxf'(cosx)
=> g'(x) = f'(sinx)(cosx - sinx)
ab...
cosx-sinx >0 for 0,pi/4 but f'(sinx)<0
=> g'(x) <0 for 0 to pi/4
and for pi/4 to pi/2 , cosx-sinx < 0 and f'(sinx)<0
so g'(x) >0
so b and c..
33g'(x) = cosx f'(sinx) - sinxf'(cosx)
f(cosx) = f(sin(Î /2-x))
=> f'(sinx) = -f'(cosx) ....... this line [7]
=>f'(cosx) = -f'(sinx) >0 .... (correct:f'(cosx)<0)
g'(x) = cosx f'(sinx) - sinxf'(cosx)
=> g'(x) = f'(sinx)(cosx - sinx).... *
...........
..........