shouldnt that be ∫1/2 r2 dθ between limits 0 and 2π?
13 Answers
well take it like this...
x=r cos θ
y=r sin θ
so the integral is y.dx
where r is already known from the formula above...
My first reaction was pi. r 2
Then i realised my mistake :)
yes prophet.. that is the better way to look at it..
I din want to write that cos many users would feel like what the heck!!
and yeah there at the top i made a small mistake..(i mean did not mention what Y is!!!!)
it should have been (Y-y) for the same x value!!!
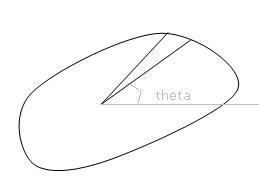
You can consider the elementary area to be these thin traingles
The area will be 1/2. base. height
base=rdθ
height =r
dA=1/2r2dθ
take the integral :)
In polar coordinates, the elemental area is 1/2 r2dθ
just as in cartesian it is y dx or xdy (actually dx dy)
to be more precise it is r dθ dr, but this will do
and x = r cos θ and y = r sin θ will not work here
Prophet it will work.. but in a slightly different way.. anyways dotn worry i have posted an explanation to why ur area works...
and yeah.. I dont disagree.. every word you have said is right :)
you may have encountered it in physics problems. but otherwise i feel its out of our syllabus
k so basically its a pizza with very small slices ...........
k understood...........in integration just as we cut into small slices in d same way here we cut into small sectors........ rite...????thts all??????
putting x=rcosθ , and y=rsinθ , I think should work but. It' involves very tedious I feel . Idint get prophet's method , nor Nishan't ?
I'll solve and post my answer