1057
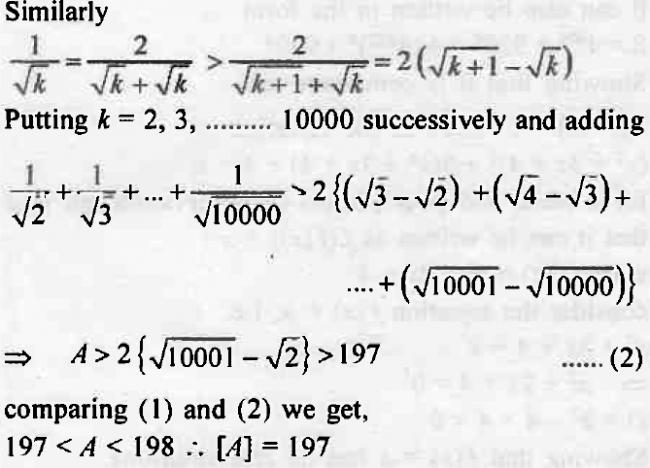
IF A=1/rt(2) + 1/rt(3) + ........... + 1/rt(10000).find [A] where [.] denotes greatest integer func nd rt stands for square root.
-
UP 0 DOWN 0 0 8
8 Answers
7A good Problem:
1 FIND THE NUMBER OF SOLUTIONS OF [X/99]=[X/101].....
2 find the total no of integral solutions of x2-2y2=2000...
1057We observe that
[X/99]=[X/101]
= 0 if and only if x ∈ {1, 2, 3, . . . , 98}, and
there are 98 such numbers. If we want
[X/99]=[X/101] =1
then x should lie in the set
{101, 102, . . . , 197}, which accounts for 97 numbers. In general, if we require
[X/99]=[X/101]=k
where k ≥ 1, then x must be in the set {101k, 101k + 1, . . . , 99(k + 1) − 1}, and there
are 99 − 2k such numbers. Observe that this set is not empty only if 99(k + 1) − 1 ≥ 101k
and this requirement is met only if k ≤ 49. Thus the total number of positive integers x for
which
[X/99]=[X/101]
is given by
98 + \sum_{k=1 }^{49}{(99-2k)}=2499
7is the answer of the 1st q 4401???
put the solution of the 2nd q first....
1057let me think for de second question nd de first answer is 2499
7OOps, i did a calcu error. yes, the ans of 1st q is 2499 provided the q asks for d total no. of +ve integral solutions only...
