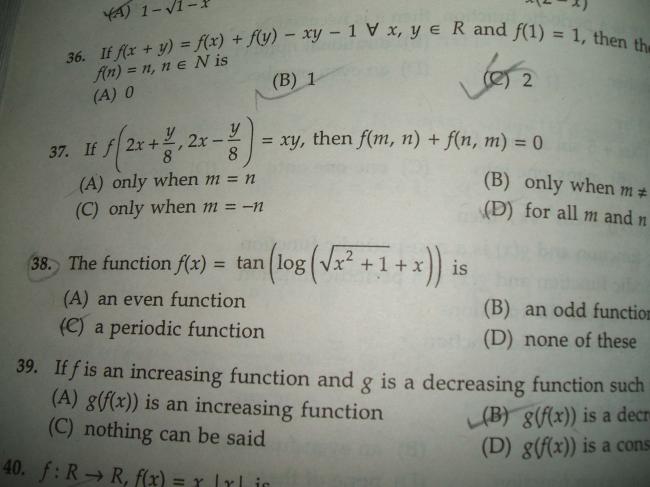1kar diye !!
I thought sir is having busy days
so why not we start a thread 4 the calculus
I will daily post question on calculus (both integral and differential)
So lets take off[1]
Q1
If [x] denotes the integral part of x , then the domain of f(x)=cos-1(x+[x]) is
(a)(0,1)
(b)[0,1)
(c)[0,1]
(d)[-1,1]
PLEASE DONT GIVE THE ANSWERS BLINDLY
DO SOLVE THEM IN THE FORUMS COMPLETELY(IF U THINK UR METHOD IS CORRECT)
-
UP 0 DOWN 0 0 34
34 Answers
1Answer for 33 is NONE OF THESE ..D
af(x) + bf(1/x) = x-1 ......... i
we can replace x by 1/x
af(1/x) + bf(x) = 1/x -1 ......... ii
add eq 1 and 2
af(x) + bf(1/x) + af(1/x) + bf(x) = x-1 +1/x -1
( a + b )( f(x) + f(1/x) ) = x + 1/x -2
f(x) + f(1/x) = ( x + 1/x -2 )/( a + b )
f(1/x) = ( x + 1/x - 2 )/( a + b ) - f(x)
substituting the value of f(1/x) in equation 1
f(x) =( x-1 - b (( x + 1/x - 2 )/( a + b )) )/(a-b)
f(2) = (2a + b)/2(a+b)(a-b) = (2a + b)/2(a2 - b2)
11yup gsns Mr Ankit was correct but i made simple question tough 4 me [1]
11@ANKIT #11
UR ANSWER IS CLOSE TO BEING PERFECT
BUT A NICE TRY
1 KE SAATH EQUALITY AAEGE
BAAKI SAB THEEK
138
Is the answer to the 38 Q, b [7][7][7]
f(x)+f(-x)=tan[log(√(x2+1)+x)(√(x2+1)-x)]/[1-log(√(x2+1)+x)log(√(x2+1)-x)]
= tan[(log1)/~]
=tan0 =0
therefore f(x)=-f(-x)
1138
f(x)=tan[log(√1+x2+x)]
-f(x)=tan\left[-log\left(\sqrt{1+x^2}+x \right) \right]
=tan\left[log\left(\frac{1}{\sqrt{1+x^2}+x} \right) \right]
rationalising, we get
=tan\left[log\left(\sqrt{1+x^2}-x} \right) \right]
which is
=tan\left[log\left(\sqrt{1+(-x)^2}+(-x)} \right) \right]
=f(-x)
i.e......f(-x)=-f(x)
Hence the answer is (b)....f(x) is an odd function [4]
1b ... [0,1) .. not in domain at x=1 .. neither below 0 ..
.. i am correct na ?
11ANKIT I NEVER SAID U TO HIDE UR ANSWERS
I TOLD U TO GIVE THE COMPLETE SOLUTION
AS PER UR OPINION CONSIDER POINT 2/3
1do u expect to solve these kinds of sums the conventional way !!
1this is not a blind answer ... yaar u r in 12 use some logic .. [50]
11U WERE RIGHT ANKIT
SORRY 4 THE INCONVENIENCE
NOW
Q2(TRY THE 1ST ONE )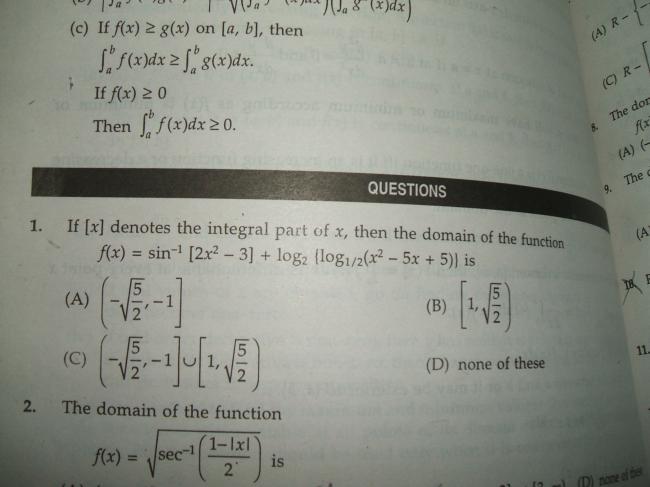
11NAHIN BHAI U R CORRECT AS USUAL
BUT PLEASE POST THE SOLUTION (ANSWER ) TO IT