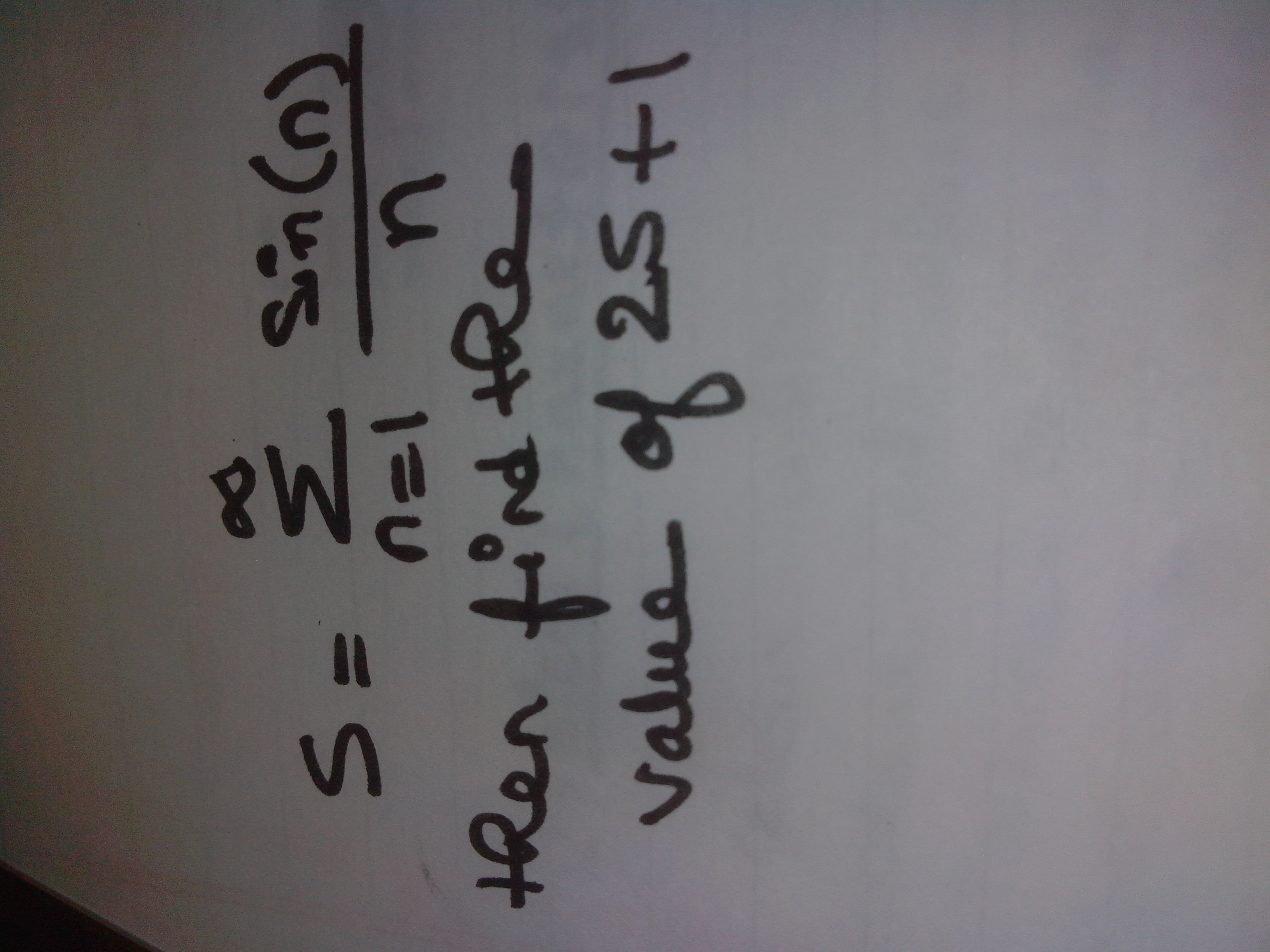\hspace{-16}$Given $\bf{\mathbb{S}=\sum_{n=1}^{\infty}\frac{\sin (n)}{n}}$\\\\\\ Now Using euler Form of Copmlex no.\\\\\\ $\bf{\cos (n)+i\sin (n)=e^{in}}$ and $\bf{\cos (n)+i\sin (n)=e^{-in}}$\\\\\\ So $\bf{\sin (n)=\left(\frac{e^{in}-e^{-in}}{2i}\right)}$\\\\\\ So $\bf{\mathbb{S}=\sum_{n=1}^{\infty}\frac{\sin (n)}{n}=\frac{1}{2i}\sum_{n=1}^{\infty}\left(\frac{e^{in}}{n}\right)-\frac{1}{2i}\sum_{n=1}^{\infty}\left(\frac{e^{-in}}{n}\right)}$\\\\\\ Now Using $\bf{\bullet \;\; \ln(1-x)=-x-\frac{x^2}{2}-\frac{x^3}{3}-.......\infty = -\sum_{k=1}^{\infty}\frac{x^k}{k}}$\\\\\\ So $\bf{\mathbb{S}=-\frac{1}{2i}\ln\left(1-e^{i}\right)+\frac{1}{2i}\ln\left(1-e^{-i}\right)}$\\\\\\ So $\bf{2\mathbb{S}=\frac{i^2}{i}\ln\left(1-e^{i}\right)+\frac{i^4}{i}\ln\left(1-e^{-i}\right)}$\\\\\\ bcz $\bf{\bullet\; i^2=-1}$ and $\bf{i^4=1}$ and $\bf{i=\sqrt{-1}}$\\\\\\
\hspace{-16}$So $\bf{2\mathbb{S}=i\left\{ln\left(\frac{1-e^i}{1-e^{-i}}\right)\right\}=i\left\{ln\left(-e^{-i}\cdot \left(\frac{1-e^{-i}}{1-e^{-i}}\right)\right)\right\}}$\\\\\\ So $\bf{2\mathbb{S}=i\cdot \ln\left(-e^{i}\right)=i\cdot \ln\left(\frac{e^{i}}{-1}\right)=i\cdot \left\{\ln(e^{i})-\ln(-1)\right\}}$\\\\\\ So $\bf{2\mathbb{S}=i\cdot \left\{\ln(e^{i})-\ln(e^{i\pi})\right\}=i\left(i-i\pi\right)=(\pi-1)}$\\\\\\ So $\bf{2\mathbb{S}=(\pi-1)\Rightarrow \boxed{\boxed{\bf{2\mathbb{S}+1=\pi}}}}$