yes if it is self orthogonal then we must get the same curve as answer wen we replace dy/dx by -dx/dy and solve it?????????
SOLVE DEM OR GIVE HINT
1. prove that the family of curves 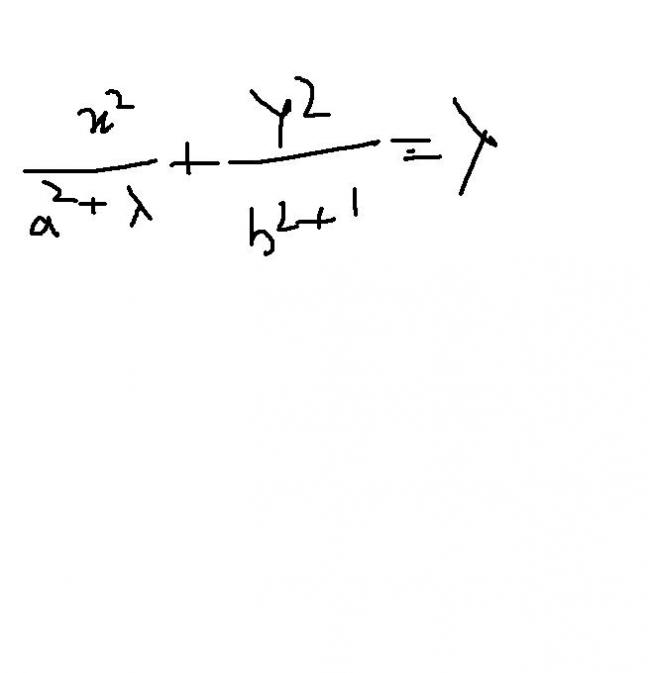
is SELF orthogonal
-
UP 0 DOWN 0 0 7

7 Answers
Take the point of intersection to be x1, x2
\frac{x^2}{a^2+\lambda_1}-\frac{x^2}{a^2+\lambda_1}=\lambda_1-\lambda_2
Or take a parametric form
solve for x..
Now,
\\\frac{x^2}{a^2+\lambda_1}+\frac{y^2}{b^2+1}=\lambda_1 \\\frac{2x}{a^2+\lambda_1}+\frac{2y\times\frac{dy}{dx}}{b^2+1}=0 \\\frac{dy}{dx}=-\frac{x(b^2+1)}{y(a^2+\lambda_1)}
You have to show that the product of both the solpes give -1
Which apparantly (without acutally solving) seems to be true from here..
just verify
didnt get properly...for chking orthogonal we replace dy/dx by -dx/dy....rit????
I thought what you were asking is that the curves or this family are orthogonal to each other...
on the other hand what you are saying is to find a family of curves orthogonal to this family of curves..
the differential equation for the system of conics is {x + y(dy/dx)}{x-y(dy/dx)} = a2-b2