1for #2,
put y = 0 and replace x-> x2 to get
f(x){sin(x2)-1} = 0
which gives us f(x) = 0.
wheres the flaw?
Title: Arihant Differential calculus Problem DOUBTS
Question Details:Attachments
In Differential Calculus by Arihant Publication
Pg.no. 88 - Q.no. 2,3,5
Pg.no. 90 - Q.no. 15,17
Pg.no. 91 - Q.no. 29
FOR THOSE WHO DONT HAVE THIS BOOK:
NOTE:
D is same as (d/dx)
f(-1)(x) is same as f inverse of x
^3 means 'power 3'
'pi' is same as 22/7 or 3.14
'sqrt.' is same as square root of
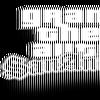
1) Let f(x) = (2x-pi)^3 + 2x - cosx. The value of D(f(-1)(x)) at x = pi is:
a) 3 pi^2 + 2
b) -2
c) 1/(3pi^2 + 2)
d) 1/3
2) A function f:R->R satisfies
sinx cosy (f(2x+2y) - f(2x-2y)) = cosx siny (f(2x+2y) + f(2x- 2y)). If f'(0)=1/2, then:
a) f''(x) - f'(x) =0
b) 4f''(x) + f(x) =0
c) f''(x) + f(x) =0
d) 4f''(x) - f(x) =0
3. If y= sec(-1)((x-1)/(x+1)) + sin(-1)((x-1)/(x+1)), then Dx=?
a) 1 b) 0
c) (x-1)/(x+1) d) (x+1)/(x-1)
4. If sqrt.(x^2 + y^2) = a e^(tan(-1)(y/x)), a>0 then y''(0) is:
a)(a/2) e^(-pi/2) b) a e^(pi/2)
c)(-2 e^(-pi/2))/a d) does not exist
5. If P(x) is a polynomial such that P(x^2+1)={P(x)}^2 + 1 and P(0)=0 then P'(0) is equal to:
a) 1 b)0
c) -1 d)none of these
6)Let f:R->R be a differential function satisfying f(y).f(x-y)=f(x) for all x,y and f'(5)=q and p.f(0)=f'(0) then f(5) is:
a) p^2/q b) p/q
c) q/p d) q.
-
UP 0 DOWN 0 0 17
17 Answers
1
1f(x)[sin(x2)] = 0 has to be true always since there was no assumption i made.
but sin(x/2) = 1 is true only at specific points.
so i think f(x) = 0 would be more general?
21that's wrong!
you can have sin(x/2) = 1 as well, say at x= pi its not required to have f(x) = 0
211) f(x) = (2x-\pi)^3 + 2x - \cos x and f^{-1}(f(x))= x \implies f^{-1}'(f(x))f'(x)= 1(*). Note that f(\frac{\pi}{2}) = \pi \vee f'(\frac{\pi}{2})= 3. Put x= \frac \pi 2 in (*) and get f^{-1}'(\pi)= \frac 1 3\; \; \blacksquare
2621. i used [f(x)]' * {[f-1(x)]'(at x=f(x)) }=1
although i dont know how i got that !!
2626. just diff. the given eqn w.r.t x and put x=y=5
we get f(5)=q/p.f(0)
now from the given eqn, we can easily say f(0)=1
hence f(5) = q/p
2623. for sin-1x , x→[-1,1]
for sec-1x x→(-∞,-1] U [1,∞)
hence the function exists only for x-1x+1 = ±1
or x =0. hence f(x) is a constant function.
thus Df(x)=0
215)Let g(x) = p(x) - x, p(0) = 0, implying g(0)= 0
P(x2+ 1) = p(x2) + 1 converts to g(x2+ 1) = g(x2)
so g(x2) = g(x2+ 1) = g(x2+ 2) = ...g(x2+ t) where t is any integer ≥ 3
so the value of the polynomial is same at infinite points , so it must be same everywhere i.e g(x) = g(0) = 0
so you get p(x) - x = g(x) = 0 or p(x) = x
so p'(x) = 1 , so p'(0) = 1
2622. simplify the given eqn as follows ,
f(2x+2y)f(2x-2y) = sin(x+y)sin(x-y)
hence we can say that f(x)=k.sin(x/2) (k=const.)
now f'(0)=k/2 =1/2
hence k=1
f(x)=sin(x/2)