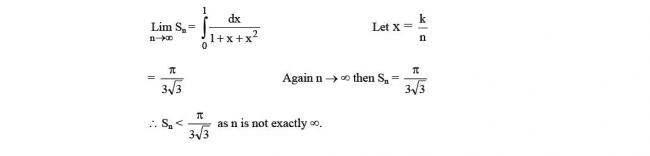Doubts in the solution!!

If you consider the function
f(x)=11+x+x²
in the interval, it is decreasing.

Divide the interval [0,1] into n equal length sub-intervals, each of width Δ = 1n by taking points
x₀ =0,
x₁ = 0+Δ = 1/n,
x₂ = 0+2Δ = 2/n
....
x_k = 0 + kΔ = k/n
x_n-1 = 0 +(n-1) Δ = n-1n, and finally
x_n = 0 + nΔ = 1.
In the k-th interval [x_k-1, x_k] for k = 1,2,..,n,
the function has a minimum value at the upper end point x_k while the maximum is achieved at the lower end x_k-1
So the lower integral sum is
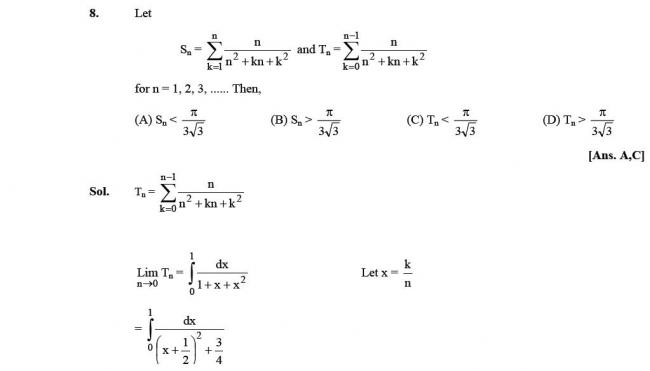
\underline{s}=\sum_{k=1}^n f(x_k)\cdot \dfrac{1}{n}=\sum_{k=1}^n f\left(\dfrac{k}{n}\right)\cdot \dfrac{1}{n}=\sum_{k=1}^n \dfrac{n}{n^2+kn+k^2}=S_n
While the supper integral sum
\overline{s}=\sum_{k=1}^n f(x_{k-1})\cdot \dfrac{1}{n}=\sum_{k=1}^n f\left(\dfrac{k-1}{n}\right)\cdot \dfrac{1}{n}=\sum_{r=0}^{n-1} \dfrac{n}{n^2+rn+r^2}=T_n
And it is known that
\underline{s}<\int_0^1 \dfrac{1}{1+x+x^2}\ \mathrm dx<\overline{s}
That is
S_n<\dfrac{\pi}{3\sqrt{3}}<T_n

The keyword is Darboux sums

http://en.wikipedia.org/wiki/Darboux_integral