with appropriate working
f(x)=\left(1+\frac{1}{x} \right)^{x}
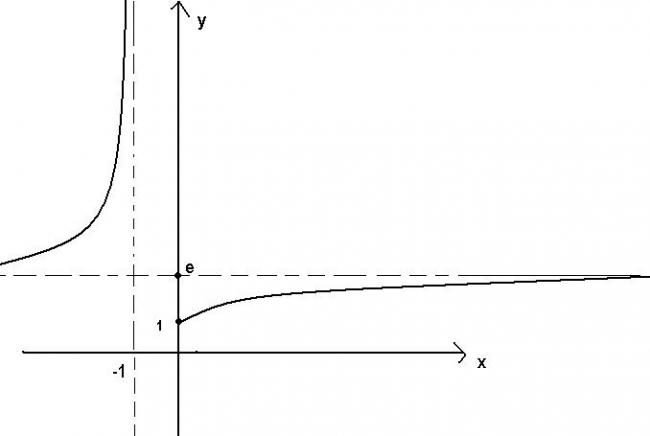
49look now in n(x) the value of the function becomes some thing at x=0
but the same value will be achieved for n(1+x) at x=-1...can u get why??
see this..x2=0 at x=0
but (x+1)2=0 at x+1=0...i.e. x=-1...isnt it??[1]
1ya point (0,1) is omitted
secondly how graph tend to e
simply bec \\\lim_{x\rightarrow+\infty }\left(1+\frac{1}{x} \right)^x=e\\ \\\lim_{x\rightarrow-\infty }\left(1+\frac{1}{x} \right)^x=e
further
\\\lim_{x\rightarrow 0^+}\left(1+\frac{1}{x} \right)^x=1\\and\\\lim_{x\rightarrow -1}\left(1+\frac{1}{x} \right)^x=\infty
1I have several questions --
1 > The point ( 0 , 1 ) should be omitted .
2 > At x = 1034 , my calculator says that f ( x ) = 1
3 > At x = 10-34 also , f ( x ) = 1
So how can the graph tend to e ?
49i have a prob in drawing the graph...can some one else help??
49indeed in my last post i was wrong....actually the function will be undefined only at such values of x where it satisfies the following conditions...
(i)it is negative
(ii)it is fractional
(iii)it has a even number in its denominator...[1]
49for the function actually in question there is more discussion to be done...
f(x)=\left(1+\frac{1}{x} \right)^{x}
in negative x axis the function as real values only at integral x not at other points...due to occurence of roots of negative qtys...
49now look as in case of 0 similarly for any arbitrary function n(x) this is true for any value
that is if n(x)=k at x=a then n(1+x)=k at x=a-1
thus the y coordinate value of n(1+x) will be equal to the y coordinate value of n(x) for the points having x coordinate equal to [{respective x-coordinate of n(x)}-1]
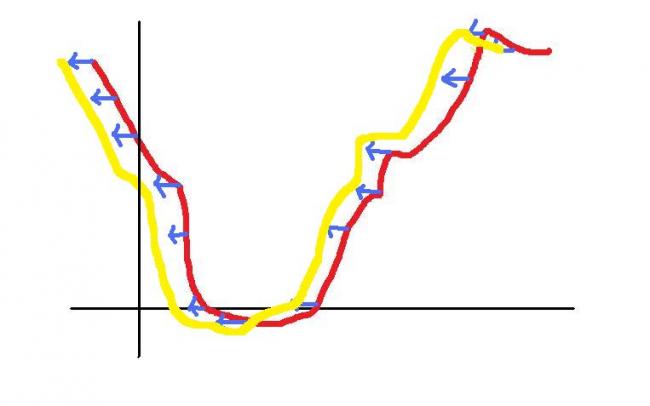
so given graph of n(x) the graph of n(1+x) can be found out by just shifting the graph towards left by 1....as shown below
6yeah i got it..u wanna say dat whn we raise a no to a power then the pt at wich it becums o shifts towards the -ve x-axis??can is say so?
49suppose the graph of n(x) is as follows....
now draw the graph of n(1+x)...[1]
49let n(x) be any arbitrary function
any arbitrary function and we have to plot the graph of n(1+x) and we have been given the graph of n(x)...[1]...thats ur question...now check out the following...[1]..
49yes kalyan i can help u out in this!!:)
check out the following posts...[1]
6i can say one thng..we draw graph of 1/x then shift it towards right by 1 unit...bt then hw to draw when it comes to power of x??
49o yeah...mai bhi gadha hu....how can we possibly take so??? the function g(x) is undefined at x=0
similarly g(1+x) is undefined at x=-1
and m(1+x) at x=-1 too...[1]
49first draw g(x)...then g(x)/x..i.e. m(x)...followed by m(1+x)...[1]
itz very difficult to graphs in laptops!!!
49LET g(x)=xx
so, g(1+x)=(1+x)1+x
so reqd graph is of m(1+x)=f(1+x)/(1+x)
thus m(x)=xx/x
evidently f(x)=m(1+x)
now this will be easy
after drawing the graph of m(x) we have to draw the graph of m(1+x)...that makes it easy right??[1][1][1]
