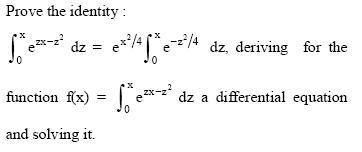66The basic idea is the generalization of the Leibniz formula:
Let
F(x)=\int_{\varphi(x)}^{\psi(x)}f(x,t)\ \mathrm dt
Then
F'(x)=f(x,\psi(x))\psi'(x)-f(x,\varphi(x))\varphi'(x)+\int_{\varphi(x)}^{\psi(x)}\dfrac{\partial f(x,t)}{\partial x}\ \mathrm dt
1L.H.S let I = \int_{0}^{x}{e^{zx}e^{-z^{2}}}dz
put z = x + t2
= \frac{1}{2}\int_{-x}^{x}{e^{\left(\frac{x+t}{2} \right)x}e^{-\left(\frac{x+t}{2}\right)^{2}}}dt
= \frac{1}{2}\int_{-x}^{x}{e^{x^{2}/2}.e^{tx/2}.e^{-x^{2}/4}.e^{-t^{2}/4}.e^{-tx/2}}dt
= \frac{1}{2}e^{x^{2}/4}\int_{-x}^{x}{e^{-t^{2}/4}}dt
= \frac{1}{2}e^{x^{2}/4}.2\int_{0}^{x}{e^{-t^{2}/4}}dt
= e^{x^{2}/4}\int_{0}^{x}{e^{-z^{2}/4}}dz=R.H.S. just substituted z inplace of t
