66That's right [1]
4 Answers
11
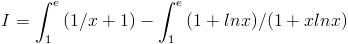
Therefore, I = [lnx + x]1 e - [lnx (1+x lnx) ] 1 e
I = e - ln (1+e)
11Didn't get when u gave this in the test, managed it while """"Reflecting - """....
\int_{1}^{e}{\frac{1+x^2lnx}{x+x^2lnx}dx}=\int_{1}^{e}{\frac{1-x}{x+x^2lnx}dx}+(e-1)
I=\int_{1}^{e}{\frac{1-x}{x+x^2lnx}dx=\int_{1}^{e}{\frac{dx}{x+x^2lnx}}-\int_{1}^{e}{\frac{xdx}{x+x^2lnx}}=I_1-I_2
2 substitutions - x=e^\theta followed by (\theta-1)=y gives
I_1=\int_{-1}^{0}{\frac{e^ydy}{e^y-y}} & I_2=\int_{-1}^{0}{\frac{dy}{e^y-y}}
I=I_1-I_2=\int_{-1}^{0}{\frac{e^y-1}{e^y-y}dy} - which is as tushar had said. [4]