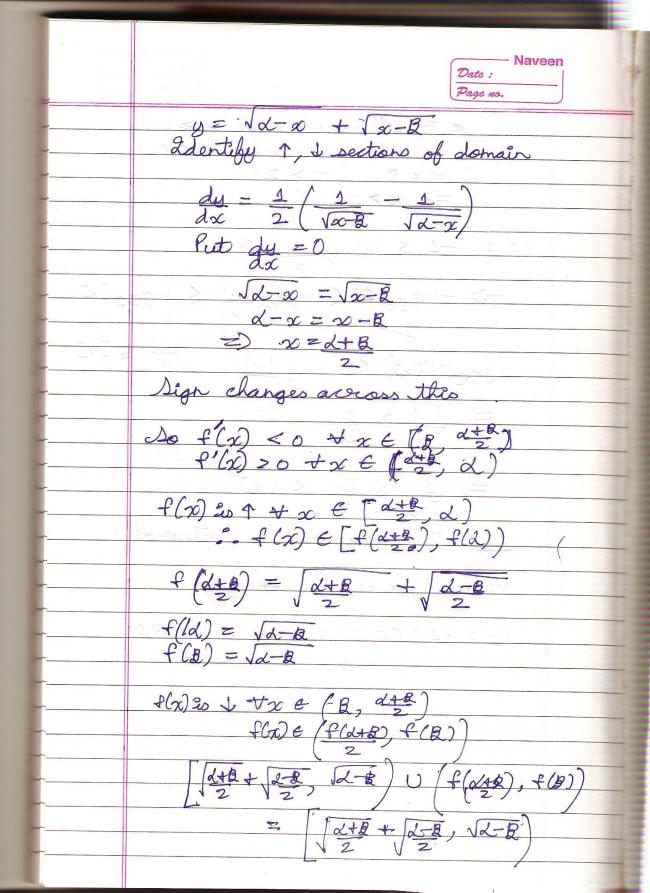Anyone there?
5 Answers
the ques is y = √f(x)
take cases
(1)x ≤ -1
(2) -1 > x ≥1
(3) x> 1
for cases (1) and (3) , the term x12 makes f(x) positive
for case (2) the term 1 ensures f(x) > 0
hence x E R
Q1. Edit : Positivity of a polynomial expression depends on the highest degree coefficient and the discriminant of the polynomial. If you say f(x) > 0 always, this means the discriminant is negative...how did you get that?
Q2.
R1 : x ≠2{x}
=> x ≠2x - 2[x]
=> x ≠2[x]
=> x2 ≠[x]
I think this is true for all x other than zero..
R2 : x - 1x - 2{x} ≥ 0
CASE I : Both Nr and Dr are positive.
x > 1 U x2 > [x]
Now x ≤ [x] < x + 1
=> 2x ≤ 2[x] < 2x + 2
So x > 2[x] is not possible for x ≤ [x] when x > 0. Thus x < 0.
x > 1 U x < 0
CASE II :
x < 1 U x < 2[x]
Applying same logic here, x > 0 U x < 1.
Apply intersection to the three cases. Not sure if I'm right here...seems a tricky question.
Q3 doesn't seem so basic..lol.
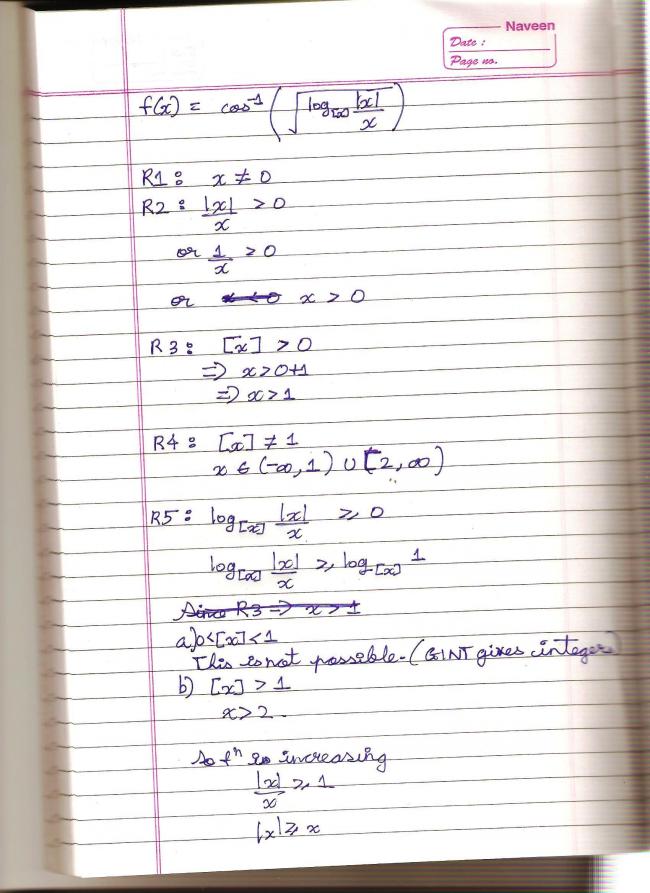
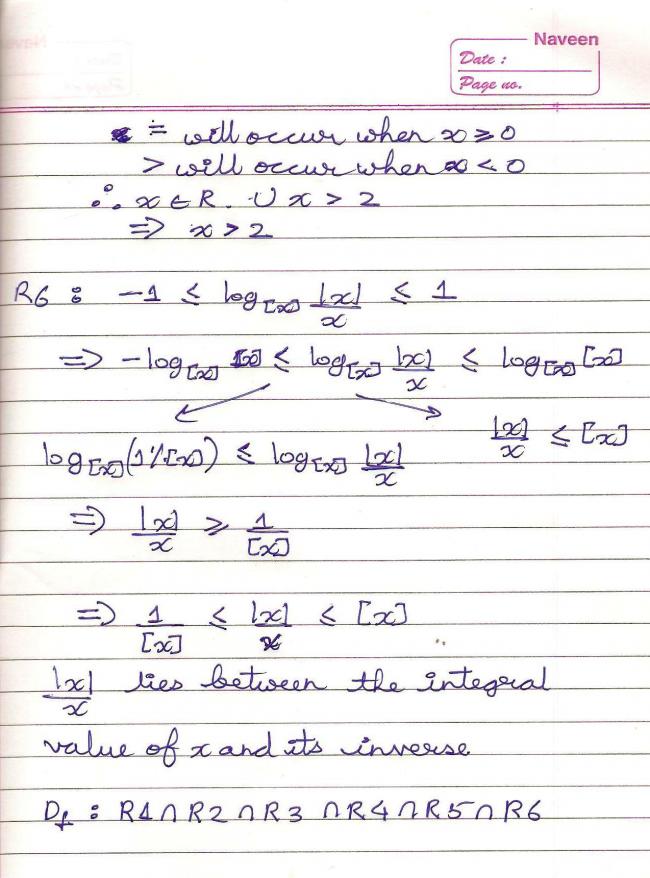
Ohh..made a mistake in R6. Root bhi toh hoga!!