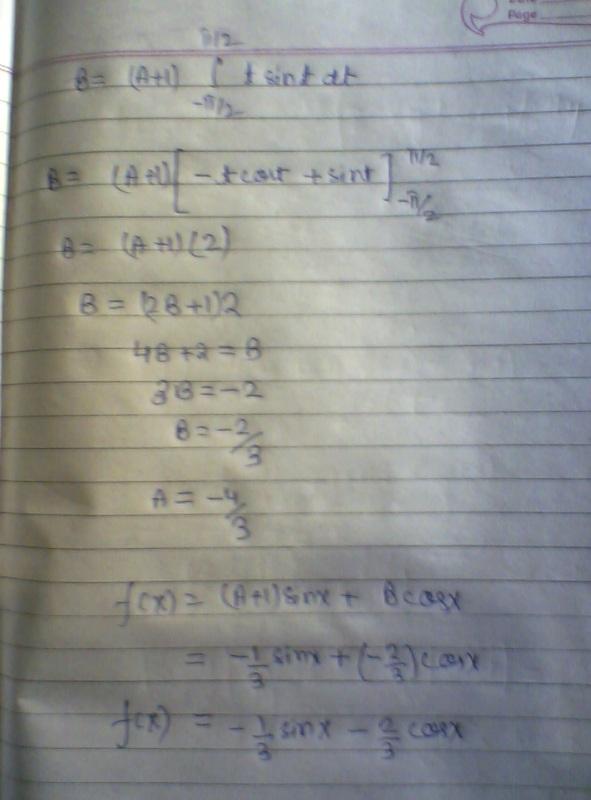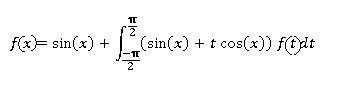11yaar dekh a+b-x wali prop nahi lagegi and its noy the one with -a to a
not getting ur words
1. f(x)=sin(x) + -π/2∫π/2((sinx+tcosx)f(t)) dt
2. 1/2∫2 sin(x-1/x) dx
x
-
UP 0 DOWN 0 0 25
25 Answers
11
11Is Q1)
f(x) = (sin x) * ∫ ....... Post #1
OR f(x) = (sin x) + ∫ ....... Post #2
[7][7][7]
62f(x)=sin(x) -π/2∫π/2((sinx+tcosx)f(t)) dt
f(x)=sin(x) -π/2∫π/2((sinx-tcosx)f(-t)) dt
Thus substracting,
-π/2∫π/2((tcosx){f(t)+f(-t)}) dt = 0
cos x is a constant so
-π/2∫π/2(t{f(t)+f(-t)}) dt = 0
will this help any bit?
I dont know!
33Q.2
I= 1/2∫2 sin(x-1/x) dx
x
Put x=1/t
I= 2∫1/2 sin(t-1/t) dx
t
I= - 1/2∫2 sin(x-1/x) dx
x
therefore I=0
33@shankara... i will post solution... tommorow... others might want to try..
Hint: keep in mind that f in f(x)=.. and inside integral are same... and write f(x)=(A+1)sin(x)+Bcos(x)... A and B are constants... of the form -pi/2∫pi/2(....) dt
11gud one
i didnt thought of that
thanks for refreshing my concepts of integeration again
33.................................................
put t=1/x in 2nd one...
................................................
3then f(x)=sinx+cosx∫tf(t)dt+sinx∫f(t)dt
f(X)=sinx+cosxt∫f(t)dt-cosx∫f(t)dt+sinx∫f(t)dt
f(x)= sinx+∫f(t)dt(sinx-cosx+cosx(∩))
f(x)=sinx+∫f(t)dt(sinx-cosx+cosx∩)
then i dunt know abi pls help after this
33:p
i don' have a doubt....
otherwise i put a "[7]" there.. :p
theres a shorter solution to that....
think definite intergral...
11look for the 2nd ques telling u the subs req
x2-1=t
2x∂x=∂t
the q will become
sin t/√t+1/2t+1
put the as they will come
if u r still in trouble then lease do tell