i have not solved it. by plotting graph in a software i m getting [ -0.52,0.5]. the method should be that of nishant. but it is too lengthy
18 Answers
see what i am saying is that we will remove all the cases where roots are outside this range
and then we will remove these cases..
Otherwise u will have to take 3 different cases as skygirl did..
i mean this is a much shorter method..
u have just say that l t l ≤ 1. then how can u show roots are > 1 in graph
yes aman.. these are the conditions i wrote in the message just above urs :)
btw u will need to find real roots' range and remove from that range the union of Case 1 and 2!
i am getting the lower limit at -.5190 using this method..
so i guess u just need to do the calculation..
it is not as lenghty as u think it is
i think it should be
case 1: k-1<0, f(1)<0 and f(-1)<0
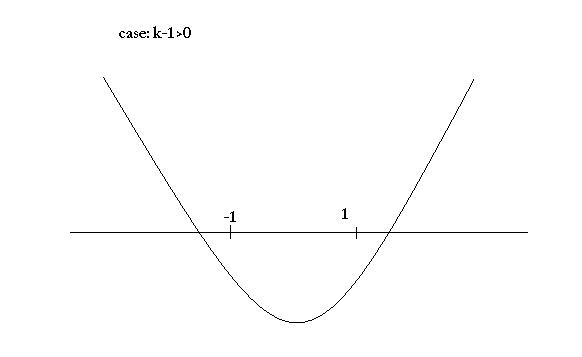
case 2: k-1>0, f(1)>0 and f(-1)>0
union of case 1 and 2
and real roots..
correct me if i m wrong
case 1: k-1>0, f(1)<0 and f(-1)<0
case 2: k-1<0, f(1)>0 and f(-1)>0
union of case 1 and 2
and real roots..
I think these 3 conditions are sufficient!
(sin2x + sinx -1)/(sin2x -sinx + 2)
= (sin2x -sinx + 2 + 2sinx - 3)/(sin2x -sinx + 2)
= 1 +(2sinx - 3)/(sin2x -sinx + 2)
we have sort of simplified it but doesnt seem to be of much use... !!!
so we will try some other trick...
sinx=t
with the condition that |t|<=1
k=(t2 + t -1)/(t2 - t + 2)
now
(t2 - t + 2)k=(t2 + t -1)
t2(k-1) - t(1+k) + 2k+1 = 0
t2(k-1) - t(1+k) + 2k+1 = 0
now u need the condition that |t| <=1
how will u incorporate that?
Hey Aman..
How did u reach -0.52? seems interesting..
May be everyone could gain from ur solution?
yes absolutely a simpler one.........
this is soomewat like finding those 'atleast' problems in probability... it should have clicked :(
neway, thank you........:)
See try this
1) find range for D>=0 (Real roots)
2) Find range for both roots outside [-1,1] ...
3) remove points in 2 from points in 1
This will give only those cases where either root is inside this range...
Ur method is right.. but i think this one will be simpler to solve :)
from here for 1). (t1+1)(t2+1) ≥0 and (1-t1)(1-t2) ≥0
similarly for rest two...
but this will be tooo long a process.... (though it was asubjective question)
i am getting three cases from graph...
1) -1<t1,t2<1 ,,,,,,
2) t1<-1, -1< t2 <1,,,,,,,,,,,
3) reverse of second....
equality will also be thr.........
Yes, first condition: real root.. then
the condition that one root should lie between -1 and 1!
That is all! (strange but true: simple looking but still not over!)