Find the minimum odd value of a

Find the minimum odd value of a for this equation to hold true

Ans) I = <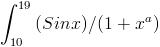

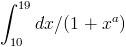
{as sinx < 1 and similarily [sinx / (1+x^a)] < [1 / (1+x^a)] }

I < <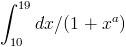
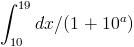
{bcoz 10 < x < 10 ........so 10 ^a+1 < 1+x^a < 19^a+1 }

So, I < 9/(1+10^a)
9 / (1+10^a) < 1/9
That implies 1+10^a > 81
10 ^a > 80
So, a=2,3,4,5,.........
Therefore, min value of 'a' = 3

U get I<91+10^a
From there how do u get 91+10^a<19 ?