1ruko 2 mins...
thik se.. copy me banate hai.. :(
Find the limit to: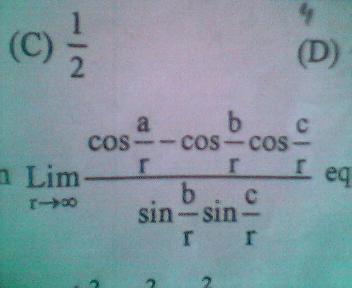
here a,b and c are non zero constants!!!!!
-
UP 0 DOWN 0 0 29
29 Answers
6another technique to finish off this question is taking a/r as t and revising the limits followed by using the formula for double angle!!!!!!!!
cheers!!!!!!!!
1it is -a^2 + b^2 + c^2 / 2bc.
did u get how to do?
if not then only i wud post ...
1) do l'hospital...
2) then divide all sin(..) by the respective angles...
1:O main bracket bhool gayi thi!!
this is the fifth asn of mine .. in this thread :O
i should get a black post [11]
6noooooooooo..........
the answer is still pending!!!!!!!!!!
@ nishant: mentor the answer is
(b2+c2-a2)/2bc
1:O yeh kaise mila??
mereko toh last time woh mila tha.. post #22...
woh bhi wrong hai!!! [2]
1Aki, by dimensionless did u mean that degree of coefficients in numerator and denominator be same even though they are constants ?
1wat y told abt dimensionless///
i din get you...
ok gving one last check
6try karo! do not waste much time!!!!!!
i have got to go for studies!!!!!!!!
catch you later!!!!!!!!!
have a nice day!!!!!!!!
bye!
6no!!!!!
but haan you are on your way!!!!!!!
the answer is having squared of a, b and c in the numerator and is dimensionless!!!!!!!!
6but there will be terms according to me such that -a/r2 which will come on applying l'hospital by the differentiation of the included angles!!!!!!!!
6i hope that you have not differentiated b/r and such terms to give -b/r2
and so on!!!!!!!!!
1how is it not ?
apply l'hospital..
then we get
L = (sina/r - sin(b+c/r))/ sin(b+c/r)
now divide and multiply with angles...
so finally:
L = a/r - (b+c/r) / (b+c)/r = a-b-c/b+c .
[edited]
6i am hanged up since 2 days!!!!!!
even here L'Hospital is applicable but ek baar lagane ke baad mann hi nahi karta kaafi lamba ho jaata hai!!!!!