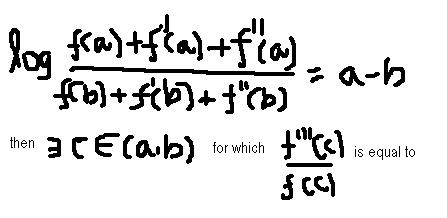111)
If these are the exact words of the qsn, then why not take f(x)=2 itself?
Check f(1)=f(√12)=f(√2)=2......
How would it have been to find all such functions......
1)Consider a differentiable function f:R→R which satisfies f2(x/√2)=f(x) for all x belongs R and f(1)=2.
Find f(x)?
2)Let f be a real function whose derivatives upto third order exist and for some pair a,b belongs R,a<b
-
UP 0 DOWN 0 2 5
5 Answers
11
1Consider function g(x) = log(f(x) + f '(x) + f ''(x))
g '(x) = f(x) + f '(x) + f ''(x)f '(x) + f ''(x) + f '''(x)
By LMVT : g '(c) = g(a) - g(b)a - b for some c belonging to (a,b)
g(a) - g(b) = log(f(a) + f '(a) + f ''(a)) - log(f(b) + f '(b) + f ''(b))
g(a) - g(b) = logf(a) + f '(a) + f ''(a)f(b) + f '(b) + f ''(b) = a - b (given)
so, g '(c) = g(a) - g(b)a - b = 1
g '(c) = f(c) + f '(c) + f ''(c)f '(c) + f ''(c) + f '''(c) = 1
f(c) + f '(c) + f ''(c) = f '(c) + f ''(c) + f '''(c)
f(c) = f '''(c)
f '''(c)f(c) = 1 for some c belonging to (a,b)
66#2: Soumik you forgot the square on the left.
The question seemingly an easy one, I haven't been able to finish it up.
I deduced the following:
1) f is not constant.
2) f(0)=1, with x=0 being an extremum.
3) f(x) > 0 for all x.
4) With F(x) = loga f(x), one gets a=2. With this transformation, the function equation reduces to the so called \mathrm{Schr\ddot{o}der} (or \mathrm{Schr\ddot{o}eder}) equation:
F\left(\dfrac{x}{\sqrt{2}}\right)=\dfrac{1}{2}\,F(x)
5) The function F(x) satisfies the condition
F(x)=2^n F\left(\dfrac{x}{(\sqrt{2})^n}\right) for each natural n.
It is easy to see that F(x)=x^2 satisfies the above condition. As such
f(x)=2^{x^2}
is a solution of the given equation. However, I haven't been able to prove the uniqueness so far (or find some other function).