why don't you look at the graph of y =|x| ?
is der ne function possible which has f'(x)=0 but it is not a constant function.
-
UP 0 DOWN 0 0 15

15 Answers
don think so ne function is possible b'coz then graph is parallel to x-axis.... which implies it wud b a constant funtion????
nooooo there's a function.will post that one within two or three days i am waiting for more replis
one q. msp ---
msp is the f(x) your talking about a real valued fn. defined for real variables ??
grandmaster i said discontinuity for the function is only at one point x=1.
Cantor function
Let us define a function f: C0[0, 1] the following way:
let bi = ai/2, then define f(x) = (0.b1b2b3...)2, where x = (0.a1a2a3...)3.
Since C0 has no isolated points, and is monotonous on C0, the extended function is actually continuous being constant on intervals of total length 1. In other words, a non constant function f that has a derivative equal to 0 on intervals of total length 1 manages to grow from 0 to 1 on the interval [0, 1]. The derivative is, of course, discontinuous; it's undefined at points of the Cantor set C0.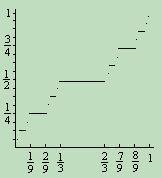
hmm it has discontinuity at more than one pt.neways i have seen a new function called contour function.
You can define your own function which is discontinuous only at x=1 and its 1st derivative is 0 elsewhere
f(x) = m when x is not equal to 1
= n when x=1
m is not equal to n and both are constants
yes sir we can define dat but this function is too much different from dat one.
the function is tan-1(x+1/x-1)-tan-1x
which has f'(x)=0 and has discontinuity at x=1.Though the function cant be find out with the hints given.I want to know whether ne one knows the function before.
sankara..
take x=tany
then you have tan-1(tan(y+pi/4) - tan-1(tan y)
which i guess is now obvious to you why its derivative is zero ;)
btw this was only a trick which the author who gave you this answer used to make you feel that it was not a constant function :D
it is not exactly constant but something like greatest integer function